---

a = np.linspace(0, 4, 100)
expo = stats.expon
lambda_ = [0.5, 1]
 
for l, c in zip(lambda_, colours):
    plt.plot(a, expo.pdf(a, scale=1. / l), lw=3, color=c, label=”$\lambda = %.1f$” % l)
    plt.fill_between(a, expo.pdf(a, scale=1. / l), color=c, alpha=.33)
 
plt.legend()
plt.ylabel(”$z$에서의 확률밀도함수(PDF)”,fontsize=13)
plt.xlabel(”$z$”)
plt.ylim(0, 1.2)
plt.title(“여러 $\lambda$값에 따른 지수확률변수의 확률밀도함수”);

---

 

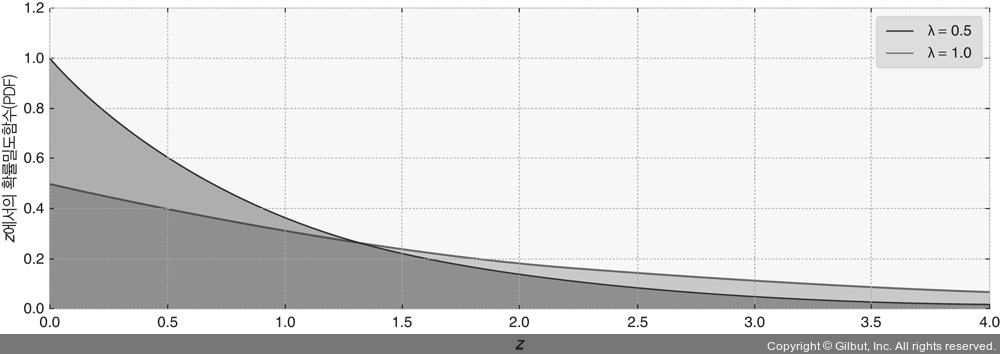
▲ 그림 1-4 여러 λ값에 따른 지수확률변수의 확률밀도함수

 

어느 지점에서 확률밀도함수 값이 그 지점의 확률과 같지 않다는 것을 알아야 한다. 이 내용은 잠시 후에 나오겠지만 만일 지금 알고 싶다면 http://stats.stackexchange.com/questions/4220/a-probability-distribution-value-exceeding-1-is-ok(단축 URL: https://goo.gl/fv2s6N)를 참고하기 바란다.