변환 행렬 우리는 변환 행렬(transition matrix)이라고 하는 2차원 행렬을 이용해 랜덤 서퍼의 행위를 모두 표현할 수 있다. 웹 페이지가 n개 있을 때 n × n 행렬을 만들어 랜덤 서퍼가 i 페이지에서 j 페이지로 이동할 확률을 i행 j열 요소에 정의한다. 먼저 표준 입력에서 데이터를 읽어 이와 같은 변환 행렬을 만드는 코드를 작성해야 한다. 90-10 규칙을 적용하면 다음과 같이 3단계로 변환 행렬을 쉽게 계산할 수 있다.

• n을 읽고 linkCounts[][]와 outDegrees[]를 생성한다.

• 링크를 읽고 i 페이지에서 j 페이지로 이동하는 링크 수의 합계를 linkCounts[i][j]에 저장하고, 페이지 i에 있는 링크 수의 합계를 outDegrees[i]에 저장한다.

• 90-10 규칙을 이용해 확률을 계산한다.

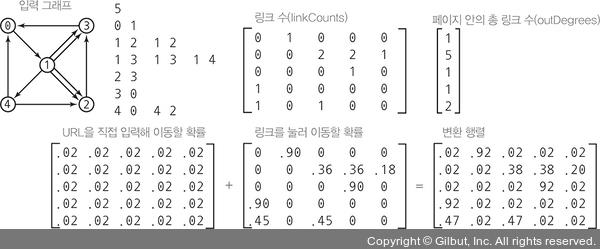
▲ 그림 1.6.3 변환 행렬 계산

 

앞의 두 단계는 상당히 간단하며, 마지막 단계도 그리 어렵지는 않다. 90-10 확률을 적용하므로, i에서 j 페이지로 이동하는 링크가 있는 경우 linkCounts[i][j]에 0.90 / outDegrees[i]를 곱하고, 모든 요소에 0.10 / n씩 더하면 된다. [프로그램 1.6.1](transition.py)은 이 계산을 모두 수행한다. transition.py는 웹 모델에서의 링크 리스트를 변환 행렬로 바꾸는 일종의 필터로 볼 수 있다.