![]() 연습 문제
연습 문제
12-1 다음 과정을 참고하여 재귀 호출을 사용한 이분 탐색 알고리즘을 만들어 보세요.
① 주어진 탐색 대상이 비어 있다면 탐색할 필요가 없습니다(종료 조건).
② 찾는 값과 주어진 탐색 대상의 중간 위치 값을 비교합니다.
③ 찾는 값과 중간 위치 값이 같다면 결괏값으로 중간 위치 값을 돌려줍니다.
④ 찾는 값이 중간 위치 값보다 크다면 중간 위치의 오른쪽을 대상으로 이분 탐색 함수를 재귀 호출합니다.
⑤ 찾는 값이 중간 위치 값보다 작다면 중간 위치의 왼쪽을 대상으로 이분 탐색 함수를 재귀 호출합니다.
![]() 잠깐만요
잠깐만요
계산 복잡도 비교
앞에서 살펴본 계산 복잡도를 표현하는 대문자 O 표기법을 계산이 간단한 것에서 복잡한 것 순으로 정리해 보겠습니다.
① O(1): 입력 크기 n과 계산 복잡도가 무관할 때
예) 계산 공식 n(n + 1) / 2를 이용한 1부터 n까지의 합(문제 1)
② O(logn): 입력 크기 n의 로그 값에 비례하여 계산 복잡도가 증가할 때
예) 이분 탐색(문제 12)
③ O(n): 입력 크기 n에 비례하여 계산 복잡도가 증가할 때
예) 최댓값 찾기(문제 2), 순차 탐색(문제 7)
④ O(n·logn): 입력 크기 n과 로그 n 값의 곱에 비례하여 계산 복잡도가 증가할 때
예) 병합 정렬(문제 10), 퀵 정렬(문제 11)
⑤ O(n2): 입력 크기 n의 제곱에 비례하여 계산 복잡도가 증가할 때
예) 선택 정렬(문제 8), 삽입 정렬(문제 9)
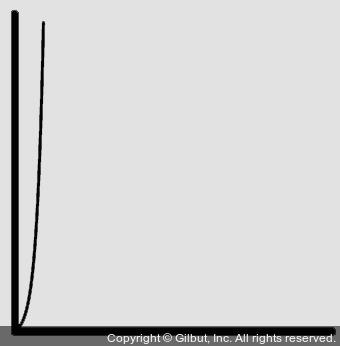
⑥ O(2n): 입력 크기가 n일 때 2의 n 제곱 값에 비례하여 계산 복잡도가 증가할 때
예) 하노이의 탑(문제 6)
|
O(1) |
O(logn) |
O(n) |
O(n·logn) |
O(n2) |
O(2n) |
|
|
그래프 |
|
|
|
|
|
|
|
n = 10 |
1 |
3.3 |
10 |
32.2 |
100 |
1024 |
|
n = 100 |
1 |
6.6 |
100 |
664.4 |
10000 |
1267650… (31자리 숫자) |
|
n = 10000 |
1 |
13.3 |
10000 |
132877.1 |
100000000 |
1995063… (3011자리 숫자) |