다른 풀이도 찾아야 한다면 (4-퀸 문제에는 풀이가 하나뿐이다) 마지막 잎에서부터 작업을 다시 속개하면 된다. 또는 체스판의 대칭성을 이용할 수도 있다.

이런 역추적은 완전 검색보다 얼마나 빠를까? 4 × 4 체스판에 있는 16개의 칸에 네 개의 퀸을 배치하는 모든 경우의 수는 다음과 같다.

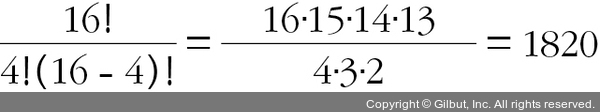
(n개의 서로 다른 객체의 집합이 주어졌을 때 순서를 따지지 않고 k개의 서로 다른 객체를 선택하는 경우의 수를 수학에서는 n개 중 k개의 조합이라고 부르는데 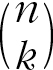또는 C(n, k)라고 쓰며 그 공식은 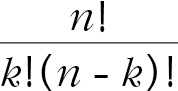이다). 퀸 네 개를 한 열에 하나씩 배치하는 경우의 수는 4⁴ = 256이다. 각 퀸이 서로 다른 행에 배치되어야 한다는 조건을 더하면 경우의 수는 4! = 24로 줄어든다. 이 정도면 그래도 해볼 만한 숫자이지만 문제가 커지면 이 값도 매우 크다. 예를 들어 8 × 8 체스판에서는 모든 퀸을 각기 다른 행과 열에 배치하는 경우의 수만 해도 8! = 40320이나 된다.

8-퀸 문제의 풀이 수는 총 92개이며 그중에서 근본적으로 다른 것은 12개이고 나머지 80개는 기본이 되는 12개를 회전하고 반사해 얻을 수 있다. 일반적인 n-퀸 문제에 대해서는 n ≥ 4인 경우, 모두 풀이가 존재하지만 임의의 n에 대해 풀이 개수를 구하는 간단한 공식은 아직 알려지지 않았다. n이 커지면 풀이 개수가 매우 빠르게 증가한다는 것만 알려졌을 뿐이다. 예를 들어 n = 10이면 풀이 개수는 724개인데 그중 92개가 근본적으로 다른 풀이이고 n = 12이면 풀이 개수는 14200개, 근본적으로 다른 풀이 개수는 1787개다.

이 책에 있는 많은 퍼즐은 역추적으로 풀 수 있다. 하지만 모든 문제를 더 효율적인 알고리즘으로 풀 수 있으며 그런 알고리즘을 찾아내는 것이 우리의 목표다. 특히 n-퀸 문제 다시 보기(2.140)에서는 n-퀸 문제를 훨씬 더 빠르게 푸는 방법을 찾아내야 한다.