분할 정복(divide-and-conquer)은 문제를 더 작은 (보통 같은, 또는 관련성 있는 유형이며 각각의 크기가 거의 같은) 부분 문제로 나눈 후 각각을 풀고 필요하면 각각의 풀이를 합쳐 원래 문제에 대한 풀이를 구하는 전략이다. 이 전략은 전산학의 여러 중요 문제를 해결하는 핵심적인 알고리즘의 바탕이다. 하지만 놀랍게도 분할 정복으로 풀 수 있는 문제가 많지는 않다. 분할 정복 전략을 완벽히 보여주는 한 가지 예를 살펴보자.

트로미노³ 퍼즐 한 칸이 빠져 있는 2ⁿ × 2ⁿ판을 직각 트로미노로 채워라. 직각 트로미노는 세 개의 맞닿은 정사각형으로 이루어지는 ㄱ 모양 타일이다. 빠지는 한 칸은 판의 어디에 있든 상관없다. 빠져 있는 칸을 제외한 모든 칸을 트로미노로 덮어야 하며 트로미노끼리 겹치면 안 된다.

이 문제는 재귀적인 분할 정복 알고리즘으로 풀 수 있다. 우선 판 중앙에 트로미노를 배치해 크기가 n인 문제 인스턴스를 크기가 n - 1인 문제 인스턴스 네 개로 분할한다(그림 1-4 참조). 이 알고리즘은 모든 2 × 2 영역이 한 개의 트로미노와 한 개의 빈칸으로 덮이면 종료된다.

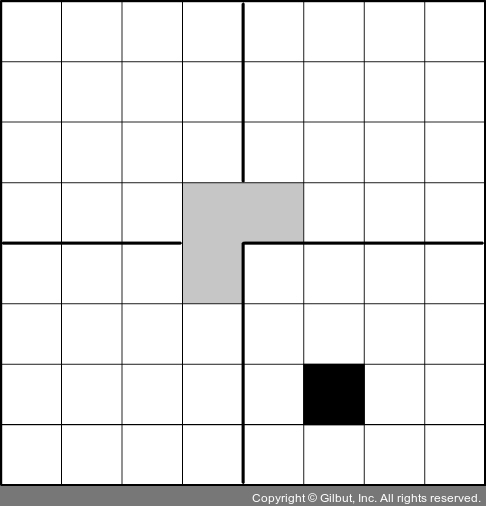
▲ 그림 1-4 한 칸이 빠진 2ⁿ × 2ⁿ판을 트로미노로 채우는 문제를 분할 정복 알고리즘으로 푸는 첫 번째 단계