이렇게 이 문제의 최적 풀이는 네 가지가 있으며(물론 대칭적으로 치환할 수도 있다) 모든 경우에 강을 건너는 횟수는 다섯 번이다.

선교사와 식인종 퍼즐(2.049)도 이 문제와 비슷하다.

그래프 표현으로 퍼즐을 푸는 것과 관련해 두 가지를 짚고 넘어가겠다. 첫째, 더 복잡한 퍼즐을 풀기 위해 상태 공간 그래프를 만드는 경우, 그래프를 만드는 것 자체가 알고리즘 면에서 중요한 문제가 될 수 있다. 사실 상태와 변의 수가 너무 많아 그래프를 만들 수 없을 수도 있다. 예를 들어 루빅스 큐브 퍼즐의 상태를 그래프로 표현하면 꼭짓점 수가 10¹⁹개가 넘어간다. 둘째, 그래프의 꼭짓점을 나타내는 점의 구체적인 위치는 이론적으로 중요하지는 않지만 평면 위에 꼭짓점을 잘 배치하면 퍼즐을 훨씬 쉽게 풀 수 있다. 다음과 같은 퍼즐을 생각해보자. 이 문제는 1512년 Paulo Guarini가 만든 것으로 알려졌지만 실제로는 840년경에 만들어진 아랍의 체스 관련 문헌에서도 발견된 적이 있다.

구아리니 퍼즐 3 × 3 체스판에 나이트 네 개가 있다. 흰색 나이트 두 개는 아랫줄 양 끝에, 검은색 나이트 두 개는 윗줄 양 끝에 있다(그림 1-6). 흰색 나이트는 윗줄 양 끝으로 가고 검은색 나이트는 아랫줄 양 끝으로 가도록 맞바꿀 수 있는 방법 중 이동 횟수가 최소인 방법을 구하라.

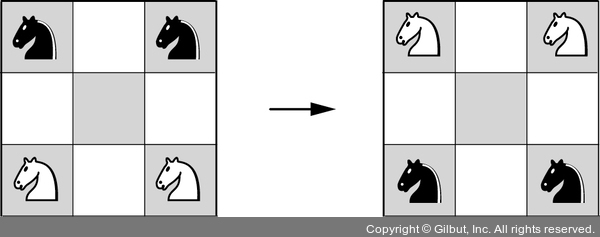
▲ 그림 1-6 구아리니 퍼즐