체스판에 있는 정사각형(편의상 그림 1-7 (a)에 나와 있는 것처럼 1부터 9까지의 정수를 붙여주자)을 그래프의 꼭짓점으로 표시하고 나이트가 이동할 수 있는 정사각형들을 변으로 서로 이어주는 방법을 자연스럽게 떠올릴 수 있다. 꼭짓점들을 체스판에 있는 사각형의 위치와 비슷하게 배치하면 그림 1-7 (b)의 그래프를 만들 수 있다(체스판 중앙에 있는 5번 정사각형에는 어떤 나이트도 갈 수 없으므로 생략했다). 그림 1-7 (b)에 있는 그래프는 문제를 푸는 데 별 도움이 안 돼 보인다. 하지만 1번 꼭짓점에서 시작해 나이트를 움직여 갈 수 있는 정사각형들을 그림 1-7 (c)에 나와 있는 것처럼 배치하고 나면 문제를 풀기가 훨씬 쉽다.⁶ 그림 1-7 (c)를 보면 나이트를 움직일 때마다 그래프에서 시계 방향이나 반시계 방향으로 움직인다는 것을 알 수 있다. 따라서 퍼즐을 최소한의 행마⁷ 횟수로 풀 수 있는 방법은 두 가지뿐이다. 나이트를 각 나이트가 대각선 방향 맞은편에 처음 다다를 때까지 시계 방향이나 반시계 방향으로 움직이는 것이다. 이 두 가지 대칭적인 옵션에는 말을 총 16번 옮기는 작업이 필요하다.

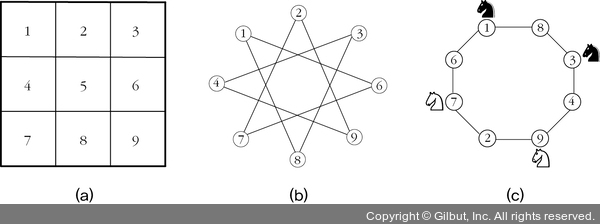
▲ 그림 1-7 (a) 구아리니 퍼즐에서 체스판의 정사각형에 번호를 매기는 방법. (b) 퍼즐의 그래프를 가장 단순하게 표현하는 방법. (c) 퍼즐의 그래프를 표현하는 더 바람직한 방법