A 교차로에서 i행(1 ≤ i ≤ 4), j열(1 ≤ j ≤ 5) 교차로까지 갈 수 있는 최단 경로 개수를 P[i, j]라고 하자. 여기서 모든 최단 경로는 수평 방향으로는 오른쪽으로, 수직 방향으로는 아래로 이동하는 식으로 만들어진다. 따라서 A 교차로에서 시작해 i행, j열로 갈 수 있는 최단 경로 개수는 A에서 i - 1행, j열로 가는 최단 경로 개수(P[i - 1, j])와 A에서 i행, j - 1열로 가는 최단 경로 개수(P[i, j - 1])를 더한 값이 된다.

1 < i ≤ 4, 1 < j ≤ 5에 대해 P[i, j] = P[i - 1, j] + P[i, j - 1]

그리고 맨 윗 줄과 맨 왼쪽 열에 대해서는 다음과 같이 된다.

1 ≤ j ≤ 5에 대해 P[1, j] = 1, 1 ≤ i ≤ 4에 대해 P[i, 1] = 1

위의 식을 이용하면 첫째 줄에서 시작해 각 줄 안에서 오른쪽으로 가면서 줄 단위로 또는 첫 번째 열에서 시작해 각 열 안에서 아래로 가면서 열 단위로 P[i, j]를 계산할 수 있다.

이 문제는 조합을 활용해 풀 수도 있다. 모든 최단 경로는 수평 선분 네 개와 수직 선분 세 개로 이루어진다. 따라서 일곱 개의 선분 중에서 수직 선분 세 개를 뽑아내는 방법에 의해 서로 다른 경로가 결정된다. 따라서 최단 경로의 총 개수는 일곱 개 중에서 세 개를 뽑아내는 경우의 수, 즉 C(7, 3) = 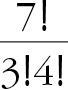= 35다.⁸ 이렇게 간단한 예제에서는 조합론을 이용한 풀이법이 동적 프로그래밍을 이용한 것보다 빠르지만 규칙성이 떨어지는 그리드에서 최단 경로 개수를 셀 때는 얘기가 달라진다. 막힌 경로 퍼즐(2.013)을 예로 풀어보자.

동적 프로그래밍을 적용하기 까다로울 때가 많지만 최대 합 내려가기(2.020), 동전 줍기(2.062)와 같은 비교적 간단한 예제를 풀어보자.