1.10.1 합 공식과 알고리즘의 효율성

사실 여부는 불분명하지만 역사상 가장 위대한 수학자 중 한 명인 Carl Friedrich Gauss (1777-1855)에 대한 유명한 일화로 이런 것이 있다. 가우스가 10살이던 무렵, 학교 선생님이 1부터 100까지 모든 정수의 합을 구하라는 문제를 냈다.

1 + 2 + ⋯ + 99 + 100

잠시만이라도 학생들을 조용히 시키고 싶었던 것 같다. 하지만 학생 중에 수학 천재가 있을 줄은 선생님도 몰랐을 것이다. 가우스는 합이 101인 50개 쌍으로 모든 수를 묶어 단 몇 분 만에 답을 구했다.

(1 + 100) + (2 + 99) + ⋯ + (50 + 51) = 101·50 = 5050

1부터 n까지 모든 정수의 합으로 일반화시키면 다음과 같다.

1 + 2 + ⋯ + (n - 1) + n =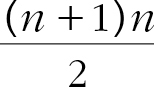

(1)

연습 삼아 이 공식과 그 유도 과정을 활용하는 암산 퍼즐(2.009)을 풀어보는 것도 좋다.

(1)번 식은 알고리즘 분석의 필수 공식 중 하나다. 이 식에서 시작해 또 다른 공식을 만들 수도 있다. 예를 들어 첫 n개의 양의 짝수는 다음과 같은 식으로 구할 수 있다.

2 + 4 + ⋯ + 2n = 2(1 + 2 + ⋯ + n) = n(n + 1)