1.10.3 재귀 알고리즘 분석

재귀호출의 고전이라고 할 수 있는 하노이의 탑 문제를 가지고 재귀 알고리즘 분석 기법을 알아보자.

하노이의 탑 이 퍼즐에서는 서로 크기가 다른 원판 n개, 기둥 세 개가 주어진다. 처음에는 원판이 모두 첫 번째 기둥에 꽂혀 있으며 가장 큰 것이 맨 밑에, 가장 작은 것이 맨 위에 크기 순서대로 꽂혀 있다. 이 퍼즐의 목적은 모든 원판을 다른 기둥으로 옮기는 것이다. 한 번에 하나씩만 옮길 수 있고 큰 원판을 작은 원판 위에 놓을 수는 없다.

이 문제는 그림 1-13에 나온 식으로 재귀적으로 풀 수 있다. n이 1보다 클 때 n개의 원판을 1번 기둥에서 3번 기둥으로 옮기려면 우선 n - 1개의 원판을 (3번 기둥을 보조 기둥으로 활용해) 1번 기둥에서 2번 기둥으로 옮기고 가장 큰 원판을 1번 기둥에서 3번 기둥으로 옮긴 후 2번 기둥에 있는 n - 1개의 기둥을 (1번 기둥을 보조 기둥으로 활용해) 3번 기둥으로 옮기면 된다. 물론 n이 1일 때는 그냥 원판 한 개를 1번 기둥에서 3번 기둥으로 옮기면 끝난다.

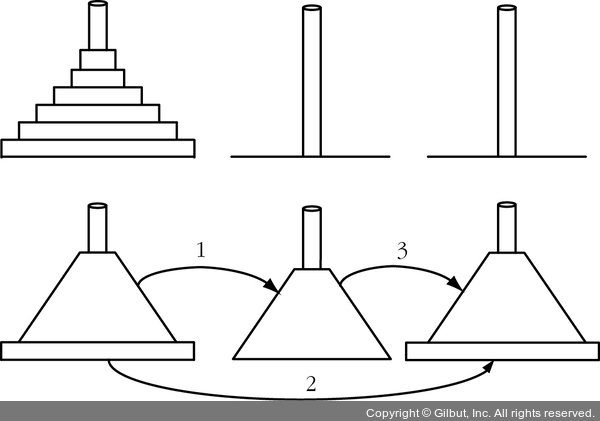
▲ 그림 1-13 하노이의 탑 퍼즐을 재귀적으로 푸는 방법