1.10.4 불변량

튜토리얼을 마무리하면서 불변량 개념을 간단히 알아보고 넘어가자. 문제를 풀 때 어떤 알고리즘을 사용하든 바뀌지 않는 속성을 불변량이라고 한다. 퍼즐형 문제에서는 어떤 불변 속성이 퍼즐의 초기 상태에 대해서는 성립하지만 최종 상태에서는 성립하지 않으므로 그 문제의 답이 존재하지 않는다는 것을 보여줄 때 불변량을 많이 사용한다. 몇 가지 예를 살펴보자.

이 빠진 체스판 도미노로 채우기 a. 귀퉁이 한 칸이 빠진 8 × 8 체스판(그림 1-14 (a))을 도미노로 채울 수 있을까? b. 대각선 방향으로 마주하는 두 귀퉁이가 빠진 8 × 8 체스판(그림 1-14 (b))을 도미노로 채울 수 있을까?

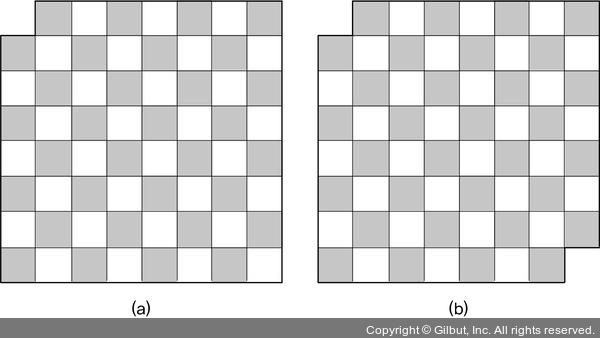
▲ 그림 1-14 (a) 귀퉁이 한 칸이 빠진 체스판. (b) 대각선 방향으로 마주하는 두 귀퉁이가 빠진 체스판