첫 번째 질문의 답은 “아니오”다. 도미노를 어떤 식으로 배치하든 도미노로 채운 칸 수는 반드시 짝수이지만 (여기서는 도미노로 채운 정사각형 개수가 짝수라는 것이 불변량이다) 체스판에 있는 정사각형 칸의 개수는 홀수다.

두 번째 질문에서는 체스판에 있는 정사각형 개수가 짝수인데도 답은 “아니오”다. 여기서는 불변량이 다르다. 도미노 한 개는 흰 칸 한 개, 검은 칸 한 개를 덮으므로 도미노를 어떤 식으로 배치하든 검은 칸과 흰 칸의 수는 같아야 한다. 이 두 귀퉁이가 빠진 판에서는 흰 칸과 검은 칸의 개수 차가 2이므로 도미노로 판 전체를 덮을 방법이 없다.

일반적으로 짝홀 특성과 색 채우기는 불변량 개념을 활용하는 가장 대표적인 예다. 이와 비슷한 퍼즐로 마지막 공(2.050), 끝에서 끝까지(2.018)와 같은 문제를 들 수 있다.

불변량의 중요성을 보여주는 또 다른 예로 프로이센의 옛 도시 쾨니히스베르크의 다리 퍼즐이 있다.

쾨니히스베르크의 다리 문제 쾨니히스베르크에 있는 일곱 개 다리를 모두 한 번씩만 건너고 시작점으로 돌아오는 방법이 있을까? 강 안에 있는 두 섬과 일곱 개 다리는 그림 1-15와 같은 식으로 연결되어 있다.

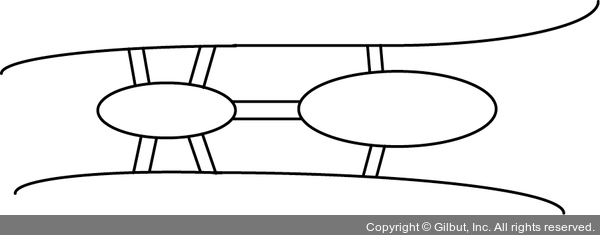
▲ 그림 1-15 쾨니히스베르크의 강가와 두 섬을 연결하는 일곱 개 다리의 연결 상태를 보여주는 그림