이 퍼즐은 스위스 태생의 위대한 수학자 Leonhard Euler(1707-1783)가 풀었다. 우선 오일러는 땅에서 걸어다니는 부분은 문제와 무관하다는 사실을 깨달았다. 중요한 정보는 다리로 연결되는 관계뿐이었다. 근대적인 개념을 사용해 말하면 이 깨달음 덕분에 오일러는 이 문제를 그림 1-16에 나와 있는 그래프 문제로 바꿀 수 있었다(정확히 꼭짓점 사이를 연결하는 변이 여러 개 있는 부분도 있으니 다중 그래프(multigraph)라고 해야 한다).

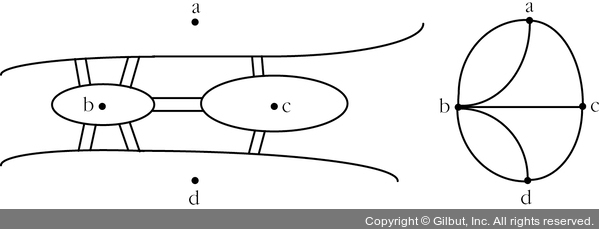
▲ 그림 1-16 쾨니히스베르크의 다리 문제를 정리한 다중 그래프

그러면 그림 1-16에 있는 다중 그래프에 오일러 회로가 있는지 따져보기만 하면 된다. 이때 오일러 회로란 한 꼭짓점에서 출발해 모든 변을 정확히 한 번씩 지나 출발점으로 돌아오는 꼭짓점의 수열을 가리킨다. 오일러는 그런 회로에서는 꼭짓점에 들어간 횟수와 꼭짓점에서 나온 횟수가 똑같아야 한다는 것을 깨달았다. 따라서 오일러 회로는 꼭짓점에 연결되는 변의 개수 - 차수라고 부른다 - 가 모두 짝수인 다중 그래프에만 존재할 수 있다. 이 불변량으로부터 쾨니히스베르크의 다리 문제에는 해답이 없다는 것을 알 수 있다. 그림 1-16에 있는 다중 그래프의 꼭짓점은 모두 차수가 홀수이기 때문이다. 게다가 그 조건으로 좀 더 생각해보면 시작점과 종착점이 다르더라도 모든 다리를 한 번씩 건너는 경로가 없다는 것을 알 수 있다. 이런 경로를 오일러 경로라고 부르는데 오일러 경로가 존재하기 위해서는 시작점과 종착점을 제외한 모든 꼭짓점의 차수가 짝수여야 한다.