random 모듈의 random.random()을 이용하면 그 결과로 0~1 사이의 실수를 얻을 수 있습니다. 이 기능을 두 번 이용해 결과를 각각 x와 y에 저장한 좌표 (x, y) 는 그림 19-4에서 정사각형 안의 한 점이 됩니다. 이 점과 원점 (0, 0) 사이의 거리가 1 이하인지 따져 보면 이 점이 빗금 친 부분 안에 있는지 알 수 있습니다. 원점에서 점(x, y) 까지의 거리 d를 구하는 공식은 다음과 같습니다.

 

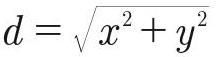
하지만 이 경우 거리가 1 이하인지를 비교하는 것이 목적이므로 굳이 제곱근을 구할 필요 없이 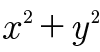의 값을 1.0과 비교하면 됩니다.

예를 들어 점 A(0.5, 0.2)를 이 공식에 대입하면, 원점과의 거리가 1 이하이므로 A는 사분원 안에 있는 점입니다.

 

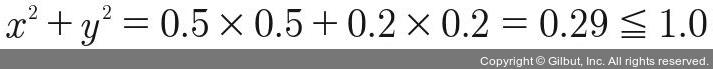
반면, B(0.8, 0.8)의 경우 원점과의 거리가 1보다 크기 때문에 사분원 밖의 점이 됩니다.

이러한 방식으로 정사각형에서 아무렇게나 한 점을 뽑았을 때, 이 점이 사분원 안에 있을 확률을 구해 보겠습니다. 실험 결과가 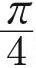와 비슷하다면, 이 결과에 4를 곱하면 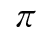와 비슷해야 할 것입니다. 정말 그런지 random모듈을 사용해서 백만 번 실험한 평균을 구해 봅시다.