III.

그날은 학원에서 함수의 극한을 복습하는 날이었다. 물론 내 처지에서는 난생처음 배우는 거라고 봐도 무방한 상황이었고.

수업 시간 내내 이어지는 외계 언어의 향연 속에서 간신히 정신 붙들고 수업에 따라가려 노력했으나, 도저히 이해되지 않는 개념 하나 때문에 머리가 자꾸만 헛도는 기분이었다.

바로 단원 초반에 나오는 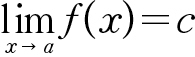라는 식이다. 선생님께서는 이 식의 의미가 “x가 a로 한없이 가까이 다가갈 때, f(x)는 c가 된다.”라고 하셨다.

f(x)는 c가 함수라는 것쯤은 나도 안다. x라는 미지수에 적당한 수를 대입하면 그에 따라 적당한 값이 나오는. 예를 들어서 f(x) = x + 1이라 하면 f(0) = 0 + 1 = 1이지.

그런데 이해할 수 없는 건, 어떻게 x가 아직 a로 ‘다가가고 있는 중’인데 f(x)의 값을 c라고 확정 지어서 말할 수 있느냐는 점이다.

아무리 x가 a에 한없이 가까워진다고 하더라도 아직 ‘정확하게’ a인 건 아니잖은가? 그러니까 f(x)도 아직 ‘정확히’ c일 리가 없고. 굳이 말한다면 c의 ‘근삿값’이라고 하는 게 맞지 않나?

이번만큼은 도저히 그냥 넘어갈 수 없었다. 나는 손을 번쩍 들고 선생님께 질문했다.

“쌤, 저거 극한이요. 어떻게 x가 정확하게 a인 상황이 아닌데 f(x)는 정확하게 c라고 하는 거예요?”