좌표 평면에 나타내 놓고 보니, 왼쪽이 아래로 향하고 오른쪽이 위를 향하는 일종의 ‘선형(선으로 표시될 만한 형태)’을 보입니다. 선형 회귀를 공부하는 과정은 이 점들의 특징을 가장 잘 나타내는 선을 그리는 과정과 일치합니다.

이 데이터에서 주어진 점들의 특징을 담은 선은 직선이므로 곧 일차 함수 그래프입니다. 일차 함수 그래프는 다음과 같은 식으로 표현할 수 있습니다.

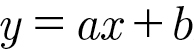
여기서 x 값은 독립 변수이고 y 값은 종속 변수입니다. 즉, x 값에 따라 y 값은 반드시 달라집니다. 다만, 정확하게 계산하려면 상수 a와 b의 값을 알아야 합니다. 따라서 이 직선을 훌륭하게 그으려면 직선의 기울기 a 값과 y 절편 b 값을 정확히 예측해 내야 합니다.

앞서 선형 회귀는 곧 정확한 선을 그려 내는 과정이라고 했습니다. 지금 주어진 데이터에서의 선형 회귀는 결국 최적의 a 값과 b 값을 찾아내는 작업이라고 할 수 있습니다.

선을 잘 긋는 것이 어째서 중요할까요? 잘 그어진 선을 통해 우리는 표 4-1의 공부한 시간과 중간고사 성적 데이터에 들어 있지 않은 여러 가지 내용을 유추할 수 있기 때문입니다. 예를 들어 표 4-1에 나와 있지 않은 또 다른 학생의 성적을 예측하고 싶다고 합시다. 이때 정확한 직선을 그어 놓았다면 이 학생이 몇 시간을 공부했는지만 물어보면 됩니다. 정확한 a 값과 b 값을 따라 움직이는 직선에 학생이 공부한 시간인 x 값을 대입하면 예측 성적인 y 값을 구할 수 있는 것입니다.

딥러닝을 포함한 머신 러닝의 예측은 결국 이러한 기본 접근 방식과 크게 다르지 않습니다. 기존 데이터(정보)를 가지고 어떤 선이 그려질지 예측한 후, 아직 답이 나오지 않은 그 무언가를 그 선에 대입해 보는 것이지요. 따라서 선형 회귀의 개념을 이해하는 것은 딥러닝을 이해하는 데 중요한 첫걸음입니다.