① 실수의 조밀성

서로 다른 두 실수 사이에는 언제나 또 다른 실수가 존재한다는 성질. 이는 곧 서로 다른 두 실수 사이에는 언제나 무수히 많은 또 다른 실수들이 존재한다는 것을 의미한다.

당연히 유리수와 무리수도 조밀성을 갖는다. 하지만 두 자연수 1 과 2 사이에 또 다른 자연수는 존재하지 않기 때문에 자연수를 비롯한 정수는 조밀성을 갖지 않는다.

※ 참고: 수의 체계

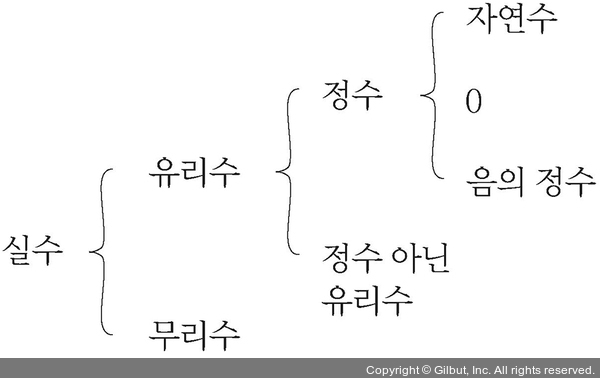
➁ 함수의 극한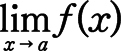

x가 한없이 a 에 가까워질 때 f(x)가 한없이 가까워지는 값. 이 값은 존재할 수도 있고(수렴), 존재하지 않을 수도 있다(발산).

함수의 극한은 엡실론(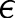)-델타(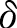) 논법으로써 엄밀하게 정의된다. 엡실론-델타 논법으로 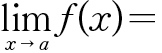c의 정의를 서술하면 다음과 같다.

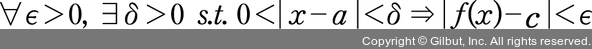
이를 우리말로 쉽게 풀어쓰면 다음과 같다.

“아무리 작은 양수를 가져와도 f(x)와 c의 차이를 그 양수보다도 작게 만들어주는 x와 a의 간격을 잡을 수 있다.”