④ 호승상소법

직역하면 ‘상호 간에 곱하여 제거하는 방법’으로, 연립일차방정식을 푸는 알고리즘이다. 본래 존재했던 방정술을 유휘가 발전시킨 방법이며, 다음은 그 내용이다.

1. 연립방정식의 계수들을 방정(方程)으로 구성한다. 예를 들어 연립일차방정식 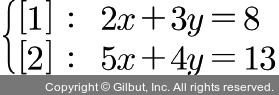을 방정으로 구성하면 다음과 같다.

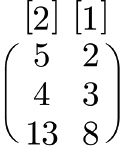
즉, 본래 '방정'의 의미는 현대 수학에서의 방정식과는 다른 개념으로, 연립방정식의 행렬표현과 유사한 것임을 알 수 있다.

2. 각 열에서 다른 열의 수를 곱하고 빼서, 0을 만드는 열 계산을 통해 삼각행렬을 얻는다.

이를 다시 연립방정식으로 구성하면 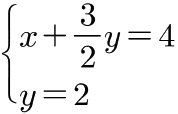이므로, 답은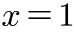 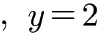이다.

3. 유휘는 2에서 별도로 각 열에 두 개의 원소만을 남기는 과정을 첨가하였다. 즉,

현대적인 관점에서 보았을 때, 2까지의 과정은 가우스소거법, 3까지의 과정은 가우스조던소거법과 그 원리가 같다.