⑤ 카발리에리의 원리

이탈리아의 수학자 카발리에리(1598년~1647년)가 발표하여 그의 이름이 붙은 원리로. 두 평면도형이 주어졌을 때, 평행한 직선에 의하며 생기는 두 선분의 길이의 비가 항상 m:n으로 일정하면 두 도형의 넓이의 비는 m:n이라는 내용이다.

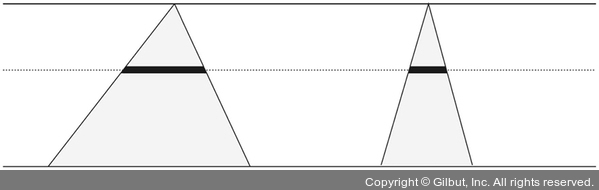
이는 공간도형의 부피에 대해서도 그대로 적용된다. 즉, 두 공간도형을 서로 평행한 평면으로 자른 단면의 넓이의 비가 항상 m:n으로 일정하면 두 도형의 부피의 비는 m:n이다.

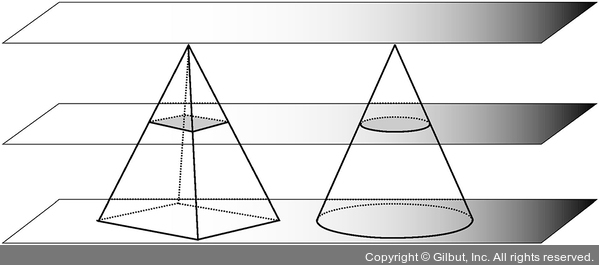
유휘는 이 원리를 이용하여 곡면으로 이루어진 입체도형의 부피를 구할 때, 그에 외접하는 다면체의 부피와 비교함으로써 간단히 구하는 방법을 구장산술에 서술하였다.