좌표 값들의 변화량도 함께 살펴봅시다.
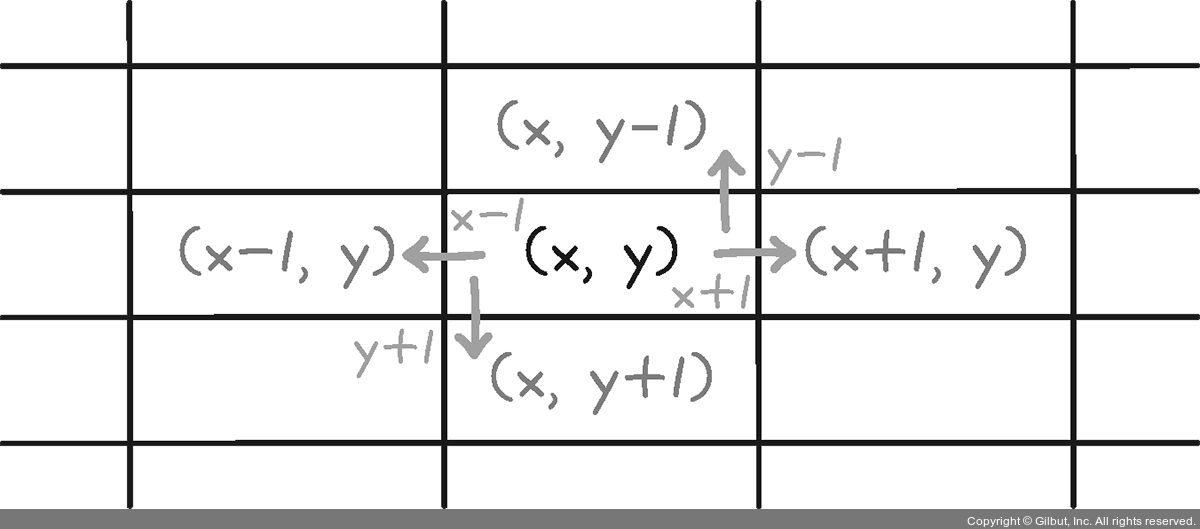
▲ 그림 3-14 (x, y)의 상하좌우로의 좌표 변화량
dx, dy는 x, y 좌표의 변화량이므로 상하좌우 네 방향에 대해서는 다음 값을 가집니다.
▼ 표 3-1 상하좌우 방향에 따른 dx, dy 값
|
|
상 |
하 |
좌 |
우 |
|
dx |
0 |
0 |
-1 |
1 |
|
dy |
-1 |
1 |
0 |
0 |
여러 개의 방향을 다루기 위해 이 값을 배열에 담으면 비로소 우리가 앞으로 다룰 dx, dy 변수가 됩니다.
private static final int[] dx = {0, 0, -1, 1};
private static final int[] dy = {-1, 1, 0, 0};
표 1-1을 그대로 배열로 옮겼으니 배열의 인덱스가 방향이 됩니다. 이 경우 인덱스 0은 상, 인덱스 3은 우 방향을 나타냅니다. 이 배열을 이용하면 위치 (x, y)를 쉽게 원하는 방향으로 이동시킬 수 있습니다. 예를 들어 다음은 (x, y)를 오른쪽으로 한 칸 이동시키는 코드입니다.
x += dx[0];
y += dy[0];
이를 응용하면 여러 방향에 대한 처리를 간단하게 표현할 수 있습니다. 앞서 살펴본 삼각 달팽이 문제를 살펴봅시다.