재귀 정의

이처럼 큰 문제를 해결하려면 작은 문제를 풀어야 하고, 문제 크기와는 관계없이 같은 로직으로 해당 문제를 해결할 수 있습니다. 각 부분 문제를 자세히 살펴보면서 다음 단계를 따라 재귀를 정의해봅시다.

1. 상태

2. 종료 조건

3. 점화식

상태

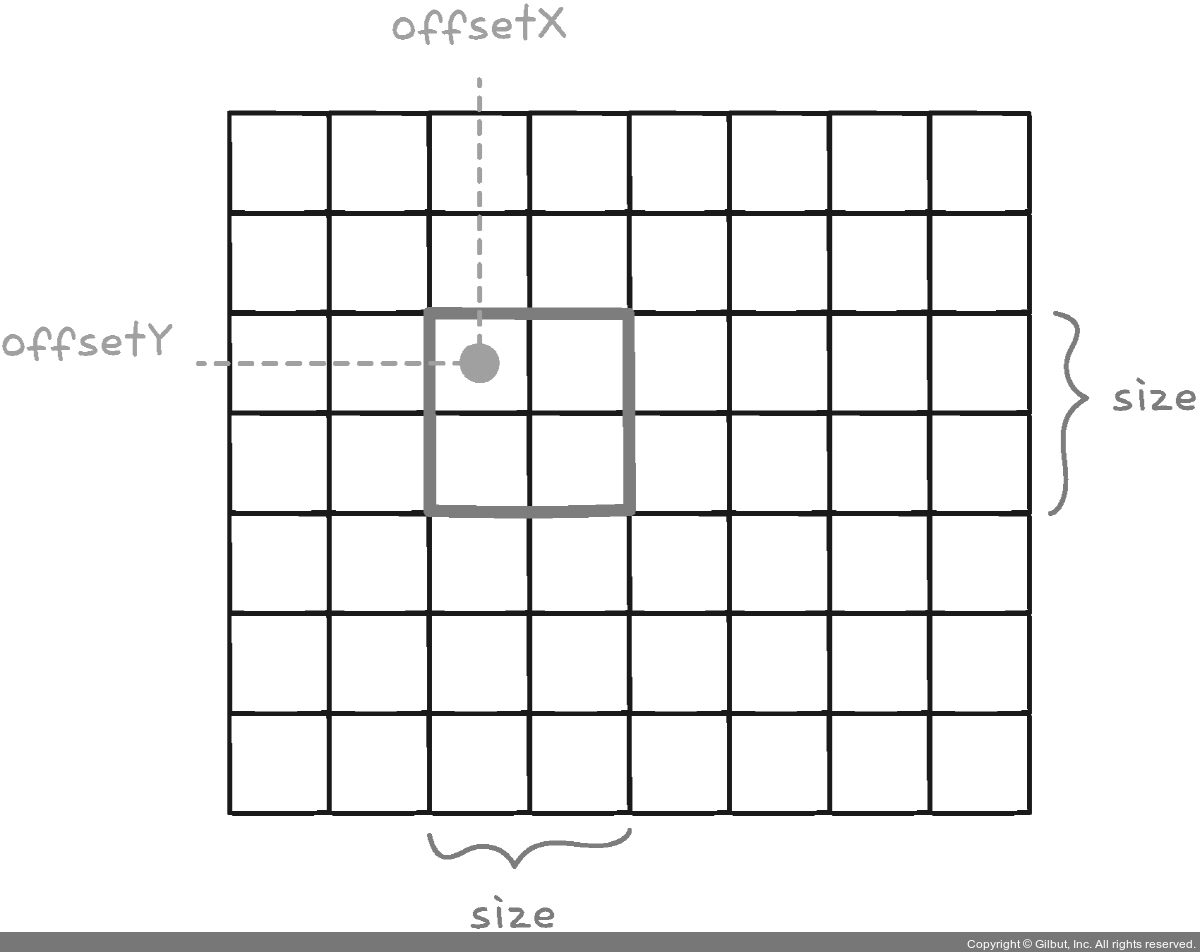
‘쿼드압축 후 개수 세기’ 문제에서는 정사각형 범위가 계속해서 분할되어 가므로 하나의 상태는 정사각형 범위를 나타냅니다. 2차원 배열에서 정사각형 범위는 정사각형이 시작하는 좌표와 한 변의 크기를 사용해서 나타낼 수 있습니다. 즉, 상태는 (offsetX, offsetY, size)처럼 나타낼 수 있습니다.

이 상태는 2차원 배열의 (offsetX, offsetY) 좌표에서 시작하여 가로 길이와 세로 길이가 size인 정사각형 범위를 나타냅니다.

▲ 그림 5-1 상태 (offsetX, offsetY, size)가 나타내는 정사각형 범위