6.5.2 히스토그램 균등화
히스토그램 균등화는 영어로는 histogram equalization이라고 하며, 히스토그램 평활화 또는 히스토그램 평탄화라는 용어로도 번역되어 사용되고 있다. 히스토그램 스트레칭이 영상의 히스토그램을 선형적으로 펼쳐주는 방식이라면, 히스토그램 균등화는 히스토그램의 누적 분포 특성에 근거하여 히스토그램의 분포를 변경시키는 방법이다. 먼저 히스토그램 균등화의 이론적인 배경에 대해서 알아보자.
영상의 픽셀 값을 변환하는 함수를 다음과 같이 표현한다고 하자.
s = T(r)
위 식에서 r은 입력 그레이스케일이고, s는 변환 함수 T에 의한 출력 그레이스케일 값이다. 일반적으로 변환 함수 T는 단조 증가 함수로 가정하며, 히스토그램 균등화도 단조 증가 변환 함수의 형태로 나타낼 수 있다. 히스토그램 균등화의 변환 함수를 제시하기 전에 먼저 몇 가지 가정을 하기로 하겠다.
앞에서 정규화된 히스토그램이 확률의 의미를 갖는다고 설명을 하였다. 이와 관련하여, 입력 영상의 히스토그램과 출력 영상의 히스토그램을 확률 밀도 함수PDF, Probability Density Function의 형태로 각각 pr(r)과 ps(s)로 나타낼 수 있다. 설명의 편의를 위해 r과 s는 연속 변수continuous variable라고 가정하자. 히스토그램 균등화의 변환 함수는 pr(r)를 누적시킨 값에 대응하는 형태로 정의되며, 다음과 같은 식으로 표현할 수 있다.
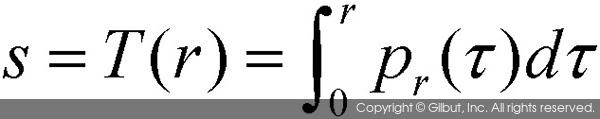
위 식에서 변수 τ는 적분을 위한 임시 변수이다. 여기서 확률 밀도 함수를 적분을 사용하여 더해준 형태의 함수를 누적 분포 함수CDF, Cumulative Distribution Function이라고 부른다. 그렇다면 이 변환 함수가 주는 의미는 무엇일까?
히스토그램 균등화를 이용하여 얻어진 결과 영상은 조금 독특한 형태의 확률 밀도 함수를 갖는다. 이를 규명하기 위해 확률 이론과 미적분 이론을 이용해보자. 확률 이론을 이용하면 pr(r)과 ps(s)의 관계를 다음과 같이 나타낼 수 있다.
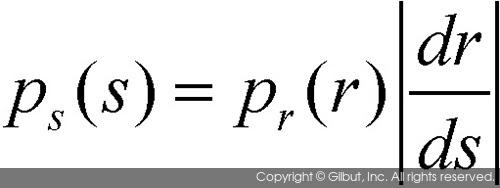
또한, s=T(r) 식에 미적분 공식을 사용하면 dr/ds의 관계를 다음과 같이 나타낼 수 있다.
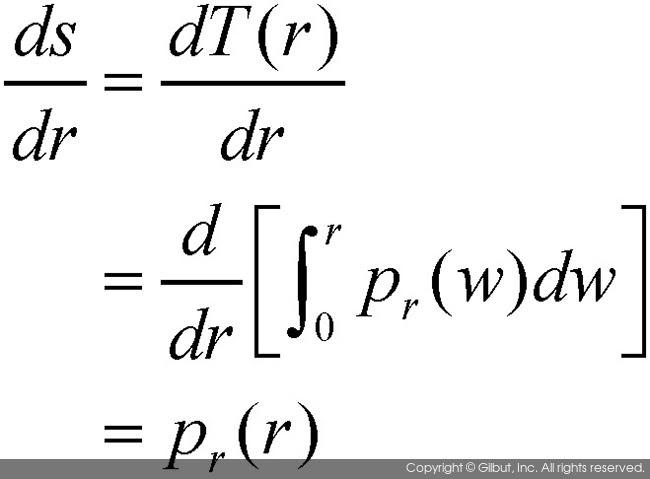
이 식을 바로 앞에 있던 식에 대입하면 ps(s)의 식을 구할 수 있다.
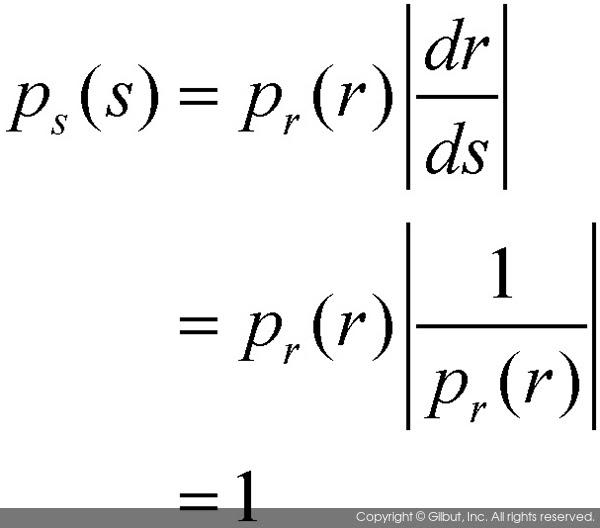
위 식에서 알 수 있듯이 히스토그램 균등화 변환 함수에 대한 출력 영상의 히스토그램은 모든 그레이스케일 값에서 1이라는 값을 가지게 된다. 히스토그램이 항상 1의 값을 갖는다는 것은 영상의 픽셀 값이 전체 그레이스케일 영역에서 균등하게 나타남을 의미한다. 즉, 모든 영상이 히스토그램 균등화 과정을 거치면 그 분포가 항상 동일한 모양으로 변하게 되는 것이다.
다만 디지털 영상에 대해 히스토그램 균등화를 수행하면 결과 영상의 히스토그램이 모든 그레이스케일 값에서 균일한 값으로 변경되지는 않는다. 대신 히스토그램 균등화가 적용된 영상에서 히스토그램 누적 그래프를 그려보면, 원점을 지나는 직선에 가까운 형태로 누적 그래프가 증가하는 것을 확인할 수 있다. 이러한 특성으로 ps(s)=1과 유사한 특성을 갖는다고 유추할 수 있다.