영상 처리에서 가우시안 필터란 이러한 2차원 가우시안 함수 값을 이용하여 마스크를 생성하고, 입력 영상과 마스크 연산을 수행하는 것을 의미한다. 원래 가우시안 함수는 연속 함수이지만, 이산형의 마스크를 만들기 위해서 x와 y 값이 정수인 위치에서만 가우시안 함수 값을 추출하여 마스크를 생성한다. 평균이 0이고 표준 편차가 σ인 가우시안 함수는 그 값의 분포가 대부분 -4σ ≤ x, y ≤ 4에서 존재하기 때문에 가우시안 필터 마스크의 크기는 (8σ+1) 형태로 결정할 수 있다. 예를 들어 그림 8-10과 같이 σ=1인 가우시안 함수를 사용할 경우, x의 값이 -4부터 +4까지, y 값도 -4부터 +4까지 존재하는 9×9 크기의 마스크를 생성할 수 있을 것이다. 그러므로 x = {-4,-3,-2,-1,0,1, 2,3, 4}, y = {-4,-3,-2,-1,0,1, 2,3, 4}인 경우에 대해 가우시안 함수 값을 계산하면 그림 8-11과 같은 가우시안 필터 마스크를 생성할 수 있다.

0.0000	0.0000	0.0000	0.0000	0.0001	0.0000	0.0000	0.0000	0.0000
0.0000	0.0000	0.0002	0.0011	0.0018	0.0011	0.0002	0.0000	0.0000
0.0000	0.0002	0.0029	0. 0131	0.0215	0.0131	0.0029	0.0002	0.0000
0.0000	0.0011	0.0131	0.0585	0.0965	0.0585	0.0131	0.0011	0.0000
0.0001	0.0018	0.0215	0.0965	0.1592	0.0965	0.0215	0.0018	0.0001
0.0000	0.0011	0.0131	0.0585	0.0965	0.0585	0.0131	0.0011	0.0000
0.0000	0.0002	0.0029	0. 0131	0.0215	0.0131	0.0029	0.0002	0.0000
0.0000	0.0000	0.0002	0.0011	0.0018	0.0011	0.0002	0.0000	0.0000
0.0000	0.0000	0.0000	0.0000	0.0001	0.0000	0.0000	0.0000	0.0000

앞에서도 잠시 언급했지만, 마스크 연산은 마스크의 크기가 커짐에 따라 그 연산 속도가 급격하게 증가한다. 그림 8-11의 경우, 마스크의 크기가 9×9 크기이기 때문에 결과 영상을 얻는 데 많은 시간을 요구한다. 요즘에는 컴퓨터의 CPU 연산 속도가 매우 빠르기 때문에 9×9 크기의 마스크 연산도 그리 느리게 느껴지지 않을 수도 있지만, 입력 영상의 크기가 커지거나 여러 장의 영상에 대하여 가우시안 필터를 수행해야 하는 경우 실시간 영상 처리 프로그램 구현에 방해가 될 수 있다.

다행히도 2차원 가우시안 함수는 1차원 함수의 곱으로 분할할 수 있기 때문에, 이를 적절하게 이용하면 빠른 가우시안 필터 구현이 가능하다. 다음 수식을 살펴보자.

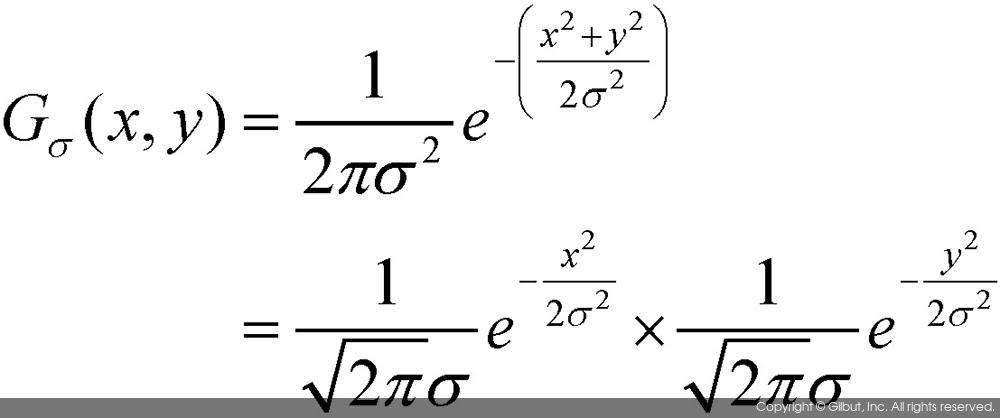
위 수식에서 2차원 가우시안 함수는 x 방향과 y 방향으로의 1차원 가우시안 함수의 곱으로 분리됨을 볼 수 있다. 이처럼 2차원 마스크를 만드는 함수를 x 방향으로의 함수와 y 방향으로의 함수로 각각 분리할 수 있을 경우, 입력 영상을 x 방향과 y 방향으로의 1차원 마스크 연산을 각각 수행함으로써 결과 영상을 생성할 수 있다.