그렇다면 영상의 이차 미분은 어떻게 구할 수 있을까? 쉽게 생각해서 영상의 일차 미분을 두 번 수행하여 구할 수 있다. 연속 함수가 아닌 이산 함수 f(x, y)에서 x 방향으로의 일차 미분은 다음의 수식으로 근사화할 수 있다.

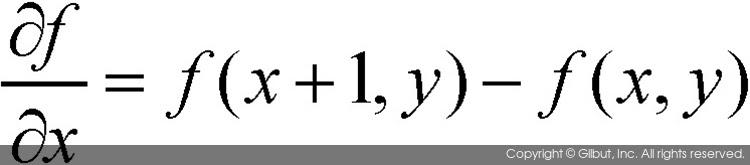
이산 함수의 이차 미분은 일차 미분 함수를 다시 한 번 미분하여 얻을 수 있다. 그러므로 함수 f를 x 방향으로 이차 편미분한 결과는 다음과 같이 표현된다.

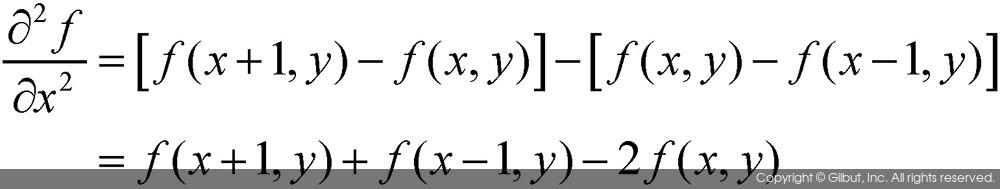
만약 함수 f를 이차원 영상이라고 할 경우, 이 영상에 대한 이차 미분 함수는 x축과 y축에 대한 각각의 이차 미분을 수행하고, 각 방향에 대한 이차 미분 결과를 합하여 구할 수 있다.

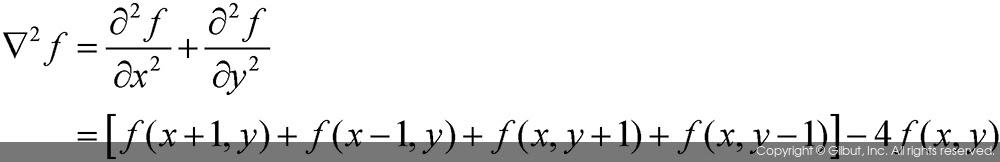
위 수식에서 ∇² 연산자가 이차 미분을 나타내는 연산자이며, 라플라시안^Laplacian 또는 델 스퀘어^{del square}라고 읽는다. 이 수식은 마스크 형태로 만들 수 있으며, 이를 그림 8-19에 나타내었다. 그림 8-19(a)의 마스크는 위 수식을 완벽하게 만족시키는 마스크이며, 그림 8-19(b)의 마스크는 함수 f를 가로, 세로, 양 대각선 방향으로 모두 미분 연산을 수행할 경우를 나타내는 마스크이다.

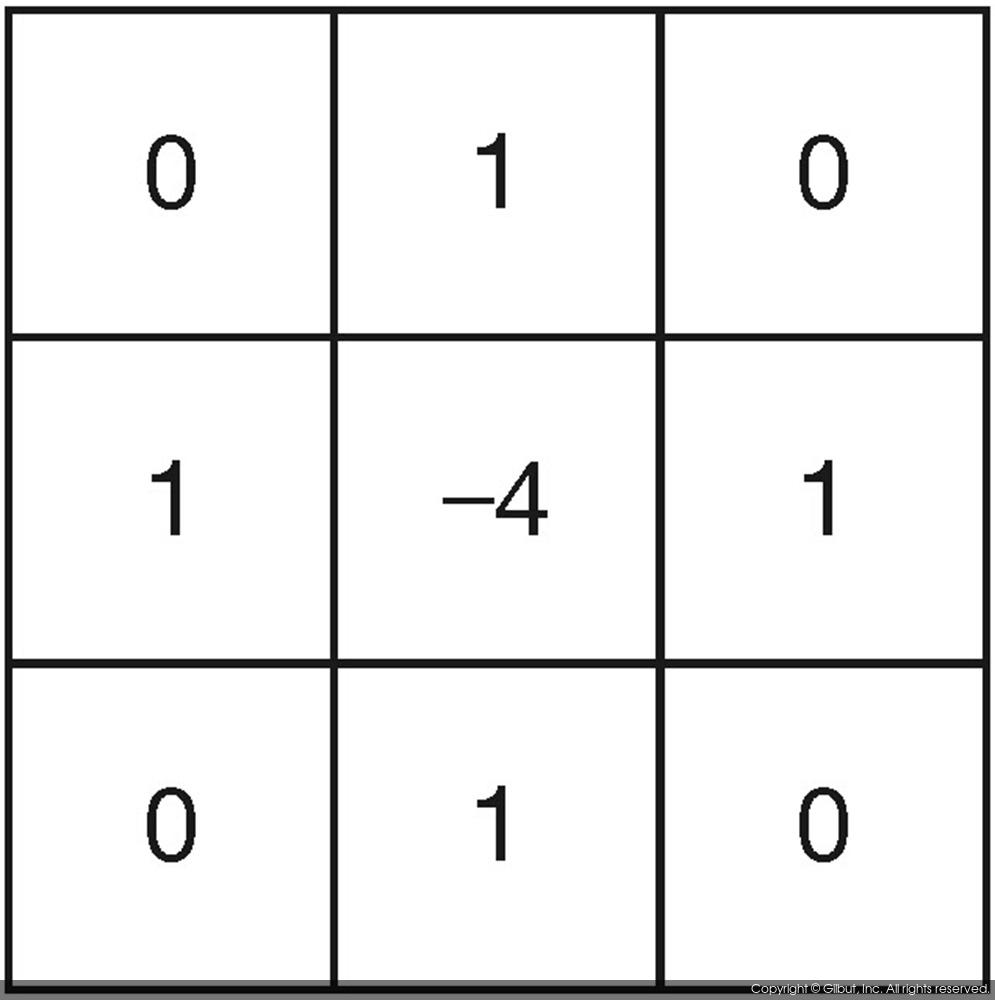
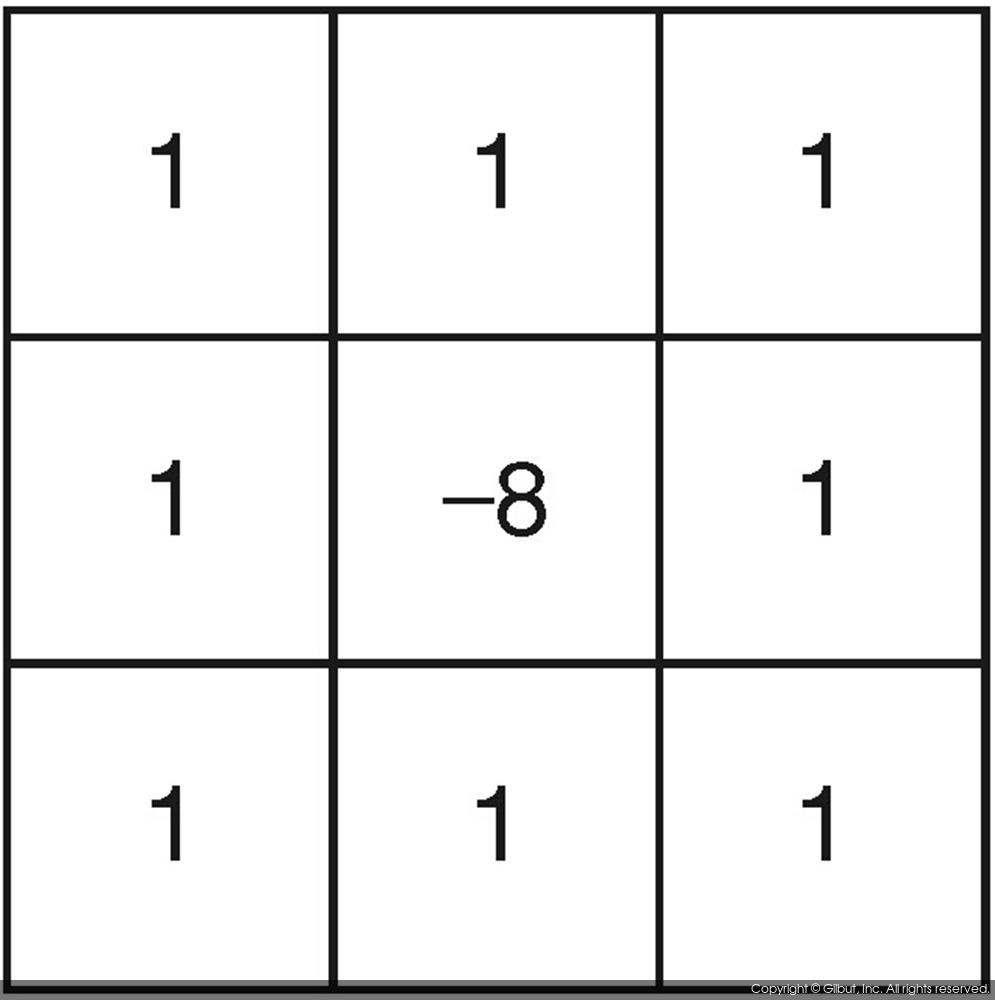
그림 8-20은 라플라시안 필터 마스크를 적용한 결과 영상의 예를 보여준다. 그림 8-20(a)의 영상은 입력 영상인 camera.bmp 파일이다. 그림 8-20(b)는 그림 8-19(a)에 나타난 마스크를 사용한 결과이고, 그림 8-20(C)는 그림 8-19(b) 마스크를 사용한 결과이다. 결과 영상에서 회색으로 나타나는 부분은 라플라시안 필터 수행 결괏값이 0에 가까운 부분이고, 엣지 근방의 흰색 또는 검정색으로 표현된 픽셀은 라플라시안 결괏값이 큰 양수 또는 음수 값을 갖는 픽셀임을 의미한다.

라플라시안을 이용하여 영상을 날카롭게 만드는 방법을 다시 수식으로 정리하면 다음과 같다.

h(x, y) = f(x, y) - ∇² f(x, y)

위 수식을 다시 풀어서 쓰면 다음과 같이 전개할 수 있다.

h(x,y) = f(x,y) - {[f(x+1,y) + f(x-1,y) + f(x,y+1) + f(x,y-1)] - 4f(x,y)}

= 5f(x,y) - f(x+1,y) - f(x-1,y) - f(x,y+1) - f(x,y-1)