8.5.3 비등방성 확산 필터
8.2절에서 소개한 영상을 부드럽게 만드는 평균 값 또는 가우시안 필터는 잡음을 제거하는 역할로 사용되기도 한다. 그러나 이들 필터는 영상의 엣지 부분 또한 부드럽게 만들기 때문에 전체적으로 영상이 흐려 보이는 단점이 있다. 1980년대 후반에 이러한 단점을 보완한 필터에 대한 연구가 진행되었다. 그 중 널리 알려진 필터는 Perona와 Malik이 제안한 비등방성 확산 필터anisotropic diffusion filter를1이다. 앞에서 가우시안과 평균 값 필터는 등방성 필터라고 소개한 바 있다. 등방성 필터가 모든 방향에 대해서 같은 정도로 부드럽게 만드는 필터링을 수행한다면, 비등방성 필터는 영상의 정보를 분석하여 각 방향의 필터링 정도를 다르게 결정한다.
비등방성 확산은 원래 물리학에서 열이 전도되는 현상에 대한 연구에서 그 수식이 유래하였다. 비등방성 확산 수식은 아래와 같다.
It = div(c(x,y,t)∇I) = c(x,y,t)△I + ∇c·∇I
위 식에서 div는 발산divergence 연산자이고, ∇와 △는 각각 그래디언트gradient와 라플라시안Laplacian 연산자이다. 라플라시안 연산자 △는 ∇2의 형태로 쓰기도 한다. 함수 c(x,y,t)는 전달 계수conduction coefficient라고 부른다. 이 책에서는 비등방성 확산 필터의 수식 유도에 대한 자세한 설명은 생략한다. 다만 비등방성 확산을 실제 영상에 적용하는 방법 위주로 설명하겠다.
비등방성 확산 수식을 디지털 영상 처리에 적용하기 위한 형태로 변경하면 다음과 같다.
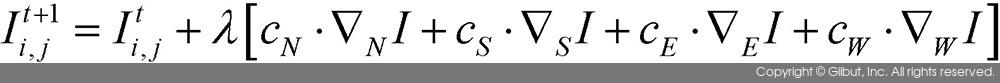
위 수식에서 영상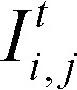 
는 시간이 t일 때 (i, j) 좌표의 픽셀 값을 의미한다. 그러므로 위 수식은 현재 (i, j) 위치의 픽셀 값이 네 방향에 대한 일차 미분에 해당하는 ∇N~WI, 그리고 cN~W 값을 이용하여 갱신됨을 의미한다. 위 식에서 λ는 픽셀 값의 변화량을 결정짓는 상수이며, 0 ≤ λ ≤ 0.25를 만족해야 한다.
네 방향에 대한 영상의 그래디언트 ∇N~WI는 다음과 같이 구할 수 있다.
▽N(Ii,j) = Ii,j-1 - Ii,j
▽S(Ii,j) = Ii,j+1 - Ii,j
▽E(Ii,j) = Ii+1,j - Ii,j
▽W(Ii,j) = Ii-1,j - Ii,j
각 수식의 아래 첨자 N, S, E, W는 각각 북, 남, 동, 서 방향을 의미한다. 이처럼 각 방향에 따라 수식이 다르게 정의되므로 비등방성이라는 수식어가 붙는 것이다. 전달 계수 함수 cN~W는 다음과 같이 구할 수 있다.
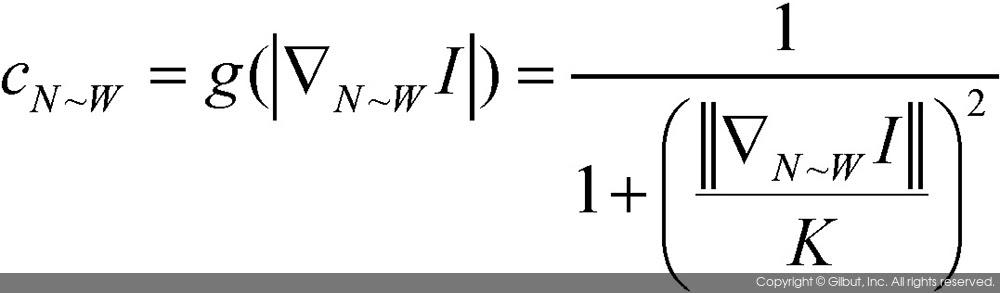
위 수식에서 상수 K는 실험적으로 지정할 수 있는 상수이며, 이 책의 구현에서는 K=4를 기본값으로 사용하였다.
1 P. Perona and J. Malik, “Scale-Space and Edge Detection Using Anisotropic Diffusion,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 12, no. 7, pp. 629-639, July 1990.