순방향 매핑의 문제점을 해결하기 위하여 일반적으로 크기 변환을 구현할 때에는 역방향 매핑^{backward mapping} 방법을 사용한다. 역방향 매핑에서는 결과 영상의 각각의 픽셀에 대하여 대응되는 입력 영상의 픽셀 위치를 찾아 그 위치에서의 픽셀 값을 참조한다. 역방향 매핑을 구현할 때에는 결과 영상의 전체 크기만큼의 for 루프를 반복하게 된다. 역방향 매핑으로 크기 변환을 수행하려면 출력 영상의 픽셀 좌표가 입력 영상의 어느 위치에 해당하는지를 계산해야 하며, 이는 다음의 수식으로 구할 수 있다.

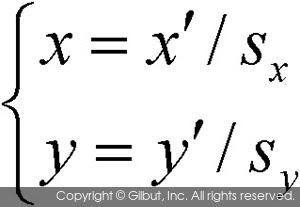
위 수식에서, x, y, x´, y´은 픽셀의 좌표를 나타내기 때문에 모두 정수이어야 한다. 그러나 x´/s_x와 y´/s_y의 계산 결과는 실수형으로 나타날 수 있으며, 이 경우 원본 영상의 어느 좌표의 픽셀 값을 참조할 것인지에 대한 결정이 필요하다. 예를 들어 그림 9-6의 예제에서 결과 영상의 (1, 1) 위치의 픽셀은 원본 영상의 (0.5, 0.5) 위치에 해당하게 되는데, 이것을 (0, 0)으로 간주해야 할지 아니면 (1, 1)로 생각해야 할지를 결정해주어야 한다. 또는 (0, 0) 픽셀 값과 (1, 1) 픽셀 값의 산술 평균을 이용할 수도 있을 것이다.

이처럼 영상의 기하학적 변환을 수행하는 경우에는 실수 좌표 상에서의 픽셀 값을 결정해야 하는 경우가 발생하며, 이때 주변 픽셀 값들을 이용하여 원하는 위치의 값을 추정하는 방법을 보간법^{interpolation}이라고 한다. 보간법에는 여러 가지 방법이 있는데, 가장 간단한 방법으로는 최근방 이웃^{nearest neighbor} 보간법이 있고, 이 외에 선형^linear 보간법, 고차 다항식^{high-order polynomial} 보간법, 스플라인^spline 보간법 등이 있다. 이 책에서는 이 중 최근방 이웃 보간법, 양방향 선형 보간법, 3차 회선 보간법에 대하여 알아보도록 하겠다.