9.2.3 양선형 보간법

양선형 보간법^{Bilinear interpolation}은 원본 영상에서 인접한 네 개의 픽셀 값을 이용하여 실수 좌표 상의 픽셀 값을 계산하는 방법이다. 양선형 보간법은 최근방 이웃 보간법에서 나타나는 계단 현상이 많이 줄어들고, 계산 방법도 간단한 편이기 때문에 널리 사용되고 있다. 양선형 보간법에서는 실수 좌표를 둘러싸고 있는 네 개의 픽셀 값에 가중치를 곱한 값들의 선형 합으로 결과 영상의 픽셀 값을 구하게 된다.

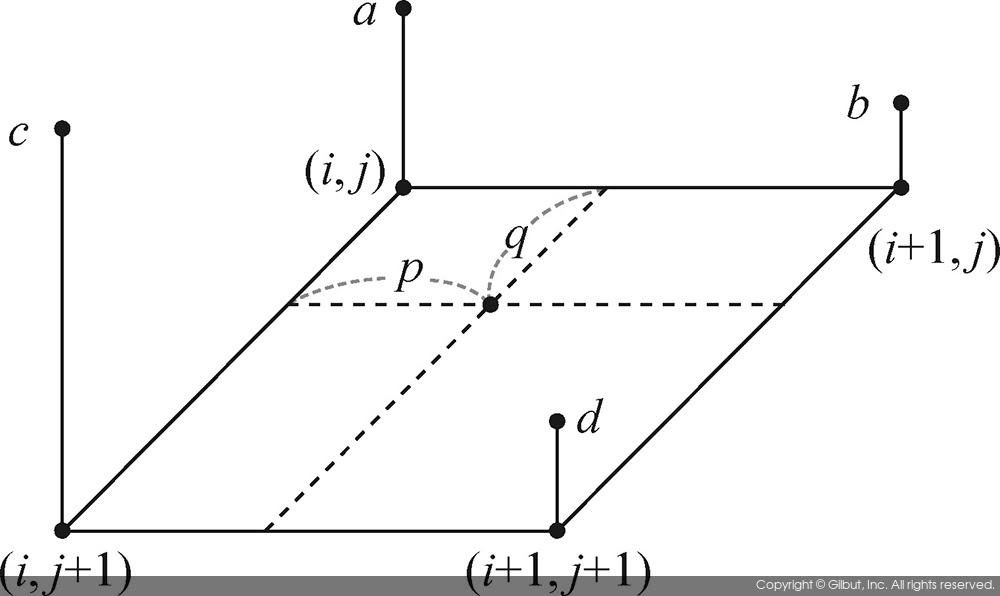
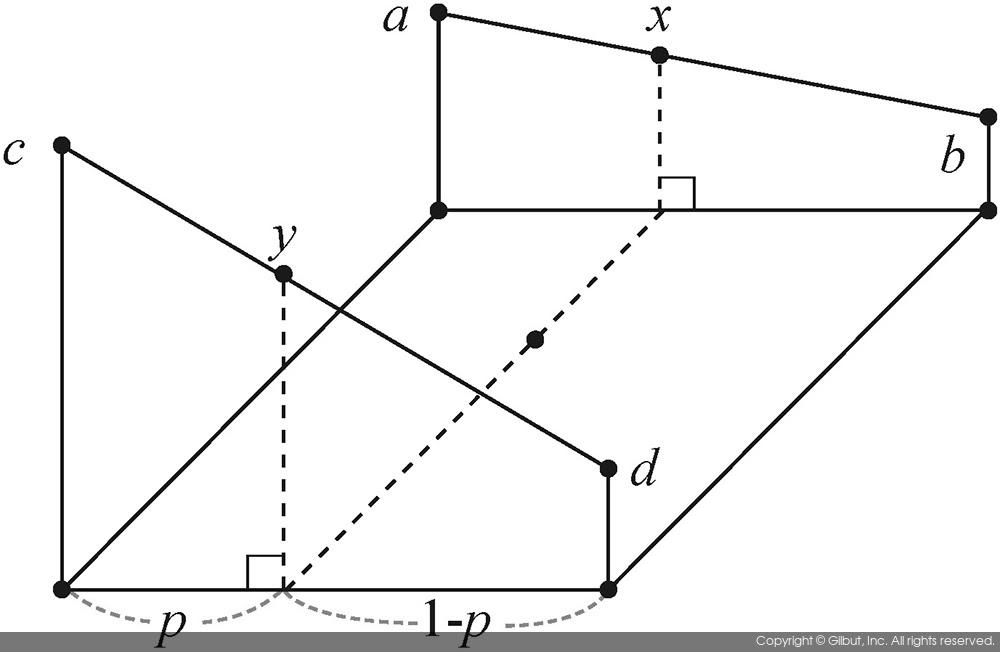
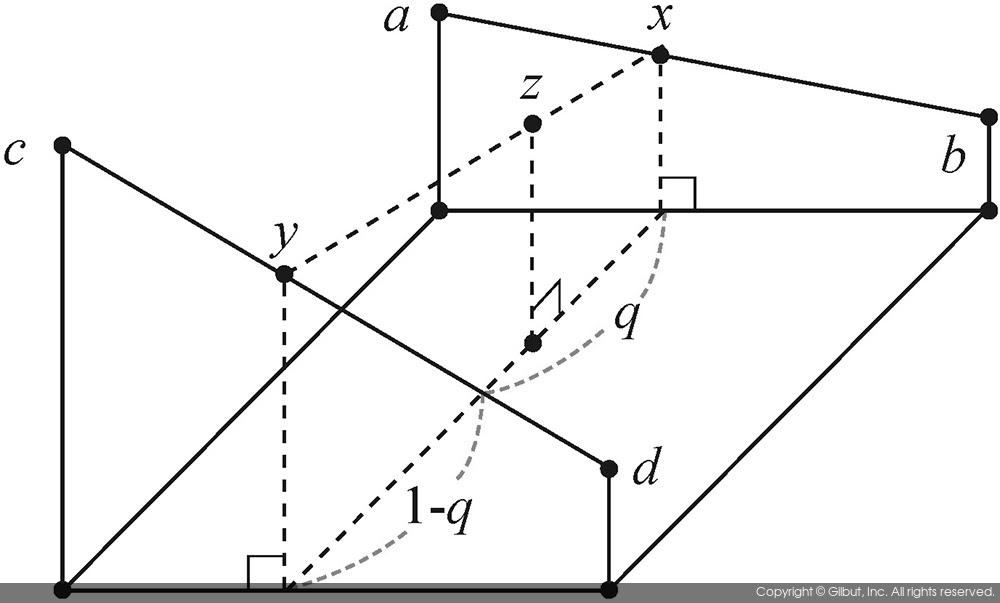
그림 9-8은 양선형 보간법에서 픽셀 값을 참조하는 방법을 보여준다. 역방향 매핑에 의해 참조해야 할 원본 영상의 좌표가 (i+p, j+q)로 결정되었다고 가정하자. 여기서 i와 j는 정수이고, p와 q는 0부터 1 사이의 실수이다. 이 실수 좌표를 둘러싼 네 개의 픽셀 좌표는 (i, j), (i+1, j), (i, j+1), (i+1, j+1)이며, 이들 좌표에서의 픽셀 값을 각각 a, b, c, d라고 하자. 이들 픽셀 좌표와 픽셀 값, 그리고 p, q의 크기를 그림 9-8(a)에 나타내었다. 양선형 보간법에서는 총 세 번의 선형 보간을 수행하게 된다. 먼저 그림 9-8(b)에 나타난 것처럼 (i, j)와 (i+1, j) 사이에서의 픽셀 값 x를 구한다. 그리고 그림 9-8(C)에 나타난 것처럼 (i, j+1)와 (i+1, j+1) 사이에서의 픽셀 값 y를 구한다. 마지막으로 그림 9-8(d)에 나타난 것처럼, 앞에서 구한 픽셀 값 x와 y를 이용하여 최종 픽셀 값 z를 구하게 된다. 결국 z 값을 결과 영상의 픽셀 값으로 사용하게 된다.

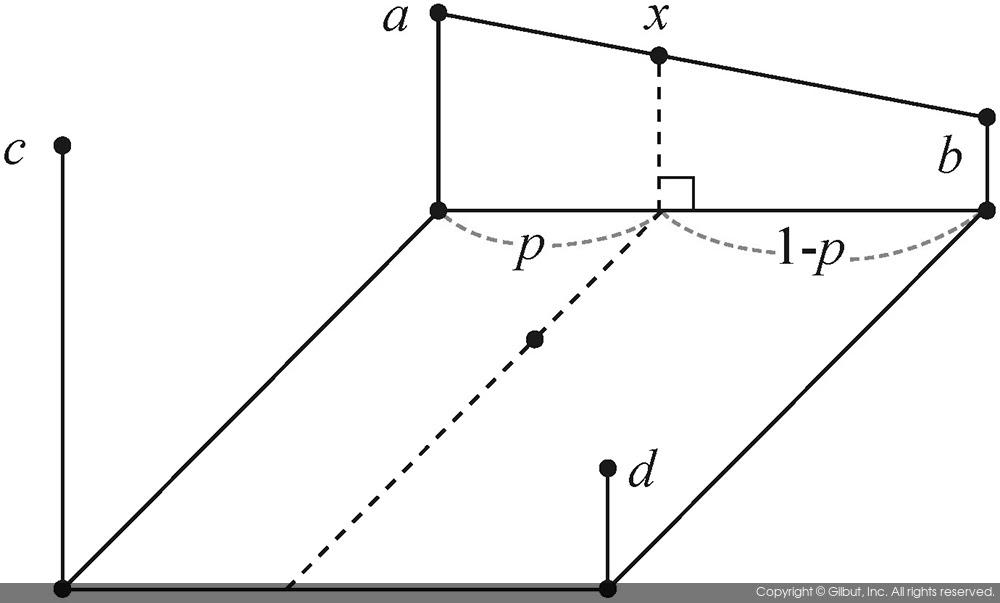
그렇다면 실제 z 값은 어떻게 구할 수 있을까? 그림 9-8(b)와 그림 9-8 (c)에서 x, y 값은 비례 법칙을 이용하여 다음과 같이 계산된다.

x = (1-p)a + pb

y = (1-p)c + pd

마찬가지로 z 값은 x, y의 값을 이용하여 다음과 같은 형태로 구할 수 있다.

z = (1-q)x + qy

위 식에서 x와 y 값을 앞의 수식으로 대체하여 정리하면 다음과 같은 하나의 식을 구할 수 있다.

z = (1-p)(1-q)a + p(1-q)b + (1-p)qc + pqd

이 수식을 그대로 C/C++ 코드 형태로 변환하면 양선형 보간법을 구현할 수 있다.

그러면 실제 양선형 보간법을 이용하여 영상의 크기 변환을 수행하는 함수를 작성해보자. 함수의 이름은 IppResizeBilinear를 사용하기로 하고, IppGeometry.h 파일에 다음과 같이 함수 선언을 추가하자.

void IppResizeBilinear(IppByteImage& imgSrc, IppByteImage& imgDst, int nw, int nh);