9.2.4 3차 회선 보간법

고차 다항식을 이용한 보간법은 가중치 함수^{weight function}를 정의하고, 원본 영상의 주변 픽셀 값에 가중치를 곱한 값을 모두 합하여 픽셀 값을 계산하는 방식을 사용한다. 이때 앞에서 설명한 양선형 보간법과 마찬가지로 각 행^row에 대하여 보간을 먼저 실시한 후, 거기서 구해진 값들을 이용하여 다시 열^column에 대한 보간을 수행하는 방식을 사용한다.

3차 회선 보간법^{cubic convolution interpolation}에서는 모두 16개의 픽셀 값을 참조하여 결과 영상 픽셀의 값을 계산한다. 그림 9-11은 3차 회선 보간법에서 사용되는 원본 픽셀들을 보여준다. 그림 중앙의 검정색 점이 결과 영상에서 참조해야 할 원본 영상의 실수 좌표라면, 그 주변의 16개의 원형 점들이 3차 회선 보간법에서 사용되는 픽셀들을 나타낸다.

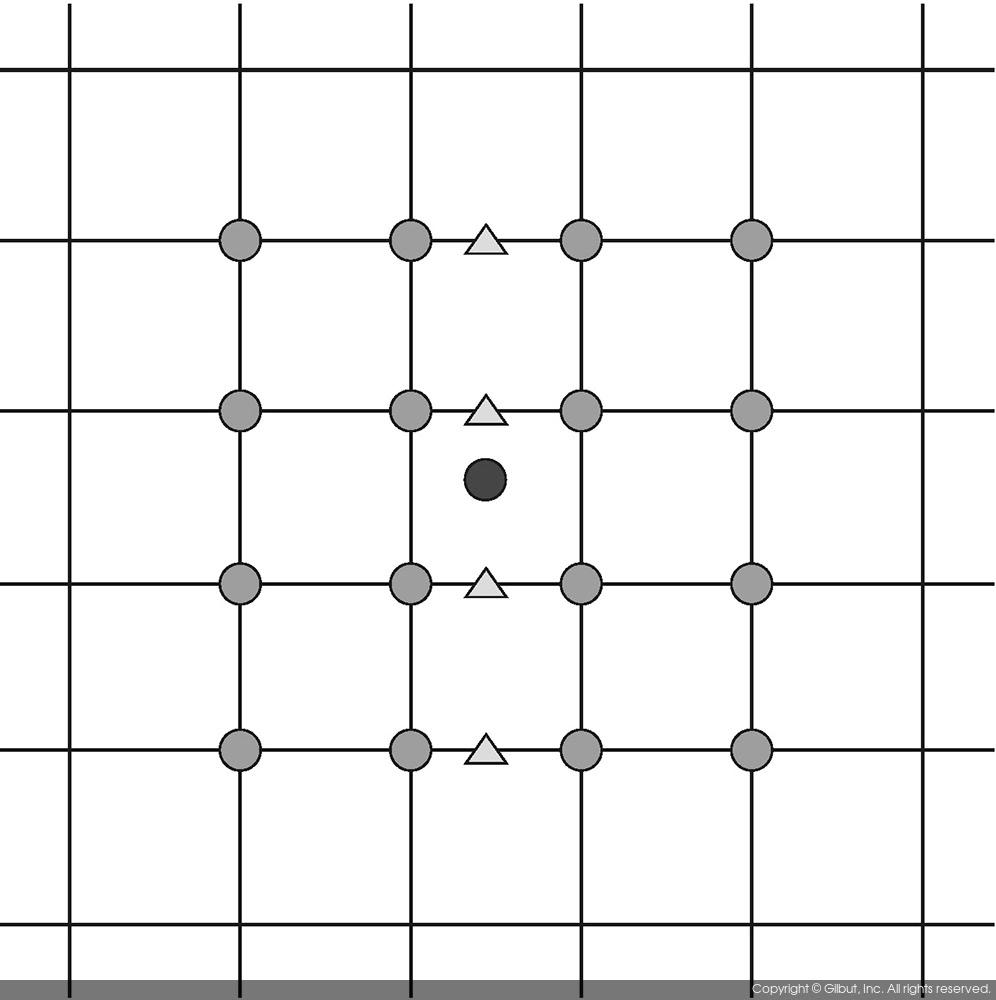
3차 회선 보간법에서는 총 5번의 보간이 이루어진다. 그림 9-11의 16개 점들을 각 행 단위로 나눠서 보간을 하여 그림 9-11의 삼각형 위치에서의 값을 추정한다. 그리고 4개의 삼각형 위치의 값을 이용하여 세로 방향으로 3차 회선 보간법을 수행하여 파란색 점 위치의 값을 추정하게 된다.

4개의 점에 대하여 3차 회선 보간법을 수행하는 방법은 다음과 같다. 3차 함수를 이용하여 4개의 점에 대한 가중치를 계산하고, 픽셀의 값과 가중치를 곱한 값들의 합으로 결괏값을 계산한다. 이 가중치 함수가 3차 곡선의 모양을 가지기 때문에, 이 보간 방법을 3차 회선 보간이라고 부르는 것이다. 3차 회선 보간에서 사용되는 가중치 함수는 다음과 같다.

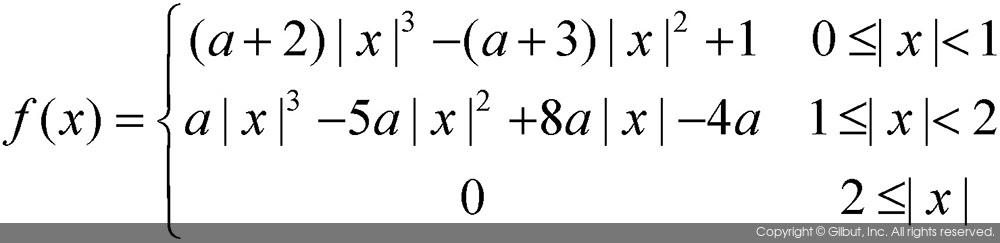
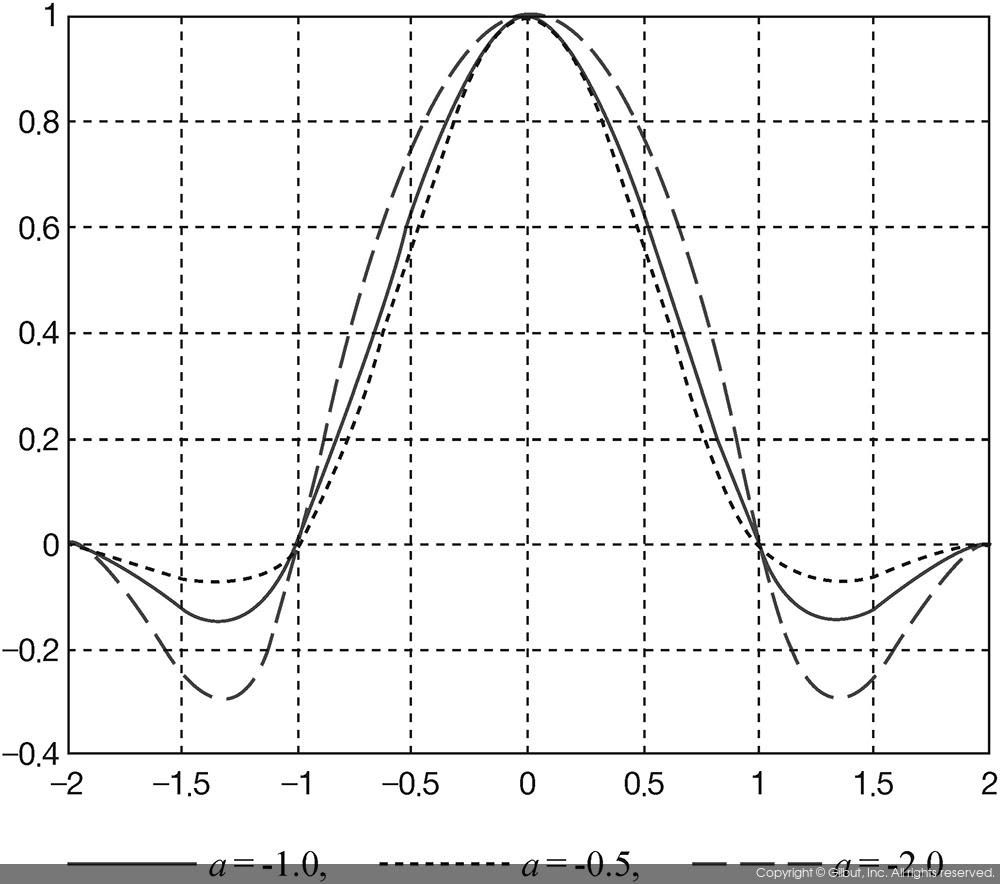
앞의 수식에서 a는 -1.0 ≤ a ≤ -0.5의 값을 주로 사용한다. a 값의 변화에 따른 3차 회선 보간법의 가중치 함수의 모양을 그림 9-12에 나타내었다. a 값이 -0.5, -1.0, -2.0으로 변함에 따라 가중치 함수가 미묘하게 변화함을 볼 수 있다. 많은 사람이 3차 회선 보간법을 구현할 때 a 값으로 -0.5를 사용한다.