10.1.1 1차원 데이터에 대한 이산 푸리에 변환

자연계에서 발생하는 모든 신호는 특정 함수들의 조합으로 표현할 수 있다. 여기서 특정 함수란 일반적인 거듭 제곱 함수 (1, x², x³,...)가 될 수도 있고, 위상이 다른 삼각함수(1,cos(θ ),cos(2θ),...)가 될 수도 있다. 이 경우 거듭 제곱 함수 또는 위상이 다른 삼각함수와 같이 조합의 기본이 되는 함수를 기저 함수^{basis function}라고 부른다. 푸리에 변환^{Fourier Transform}이란 sin 함수와 cos 함수를 기저 함수로 사용하여 입력 신호를 변환하는 방법이다. 원래 푸리에 변환은 연속 함수^{continuous function}에 대한 수학적인 접근에서 시작되었다. 그러나 이 책에서는 영상의 푸리에 변환에 초점을 둘 것이기 때문에 연속 함수가 아닌 이산 함수^{discrete function}의 푸리에 변환에 대해 자세히 알아보자.

N개의 데이터를 가지는 이산 신호 함수 f(x)(여기서 x = 0,1,2,..., N -1)가 있다고 할 때, 이 함수는 다음과 같은 푸리에 변환 공식에 의해 주파수 공간의 함수로 변환된다.

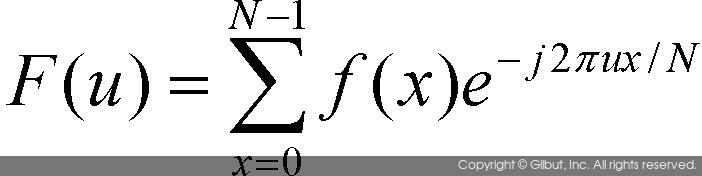
위 식에서 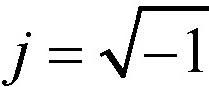이고, u=0,1,2,...,N-1의 범위를 가진다. 이처럼 이산 함수에 대한 푸리에 변환을 이산 푸리에 변환^{Discrete Fourier Transform}이라고 하며, 영어 약자로 DFT라고 한다. 이산 푸리에 변환에 의해 생성된 함수 F(u)는 다시 역변환 과정을 거쳐서 원래의 함수로 변환될 수 있다. 다음 수식은 이산 푸리에 역변환 공식이다.

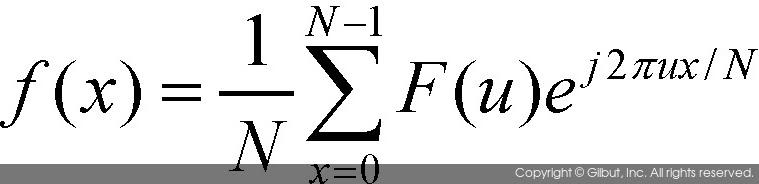
위와 같은 이산 푸리에 역변환을 영어 약자로는 IDFT^{Inverse Discrete Fourier Transform}라고 한다.

Note | DFT와 IDFT 수식 비교

DFT와 IDFT 수식은 상당히 유사하다. DFT 수식에서는 자연 지수 e의 승수에 음수 부호가 붙어 있고, IDFT 식에는 음수 부호가 붙어 있지 않은 것이 차이점이다. 그리고 IDFT 수식에는 앞에 1/N 이 들어가 있는 것을 볼 수 있는데, 이는 책마다 조금씩 기술하는 방식에 차이가 있다. 어떤 책에서는 IDFT 수식 대신에 DFT 수식에 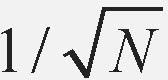을 넣어서 설명하는 책도 있고, 어떤 책에서는 DFT와 IDFT 식 모두에 1/N 을 넣어서 설명한 책도 있다. 이는 DFT로 변환된 주파수 공간의 함수가 IDFT 식에 의해 다시 역변환될 때, DFT와 IDFT 변환 공식 앞에 있는 항의 곱이 1/N 이 되어야 함을 의미한다.