10.2.1 2차원 영상의 푸리에 변환

2차원 영상의 푸리에 변환 공식은 다음과 같다.

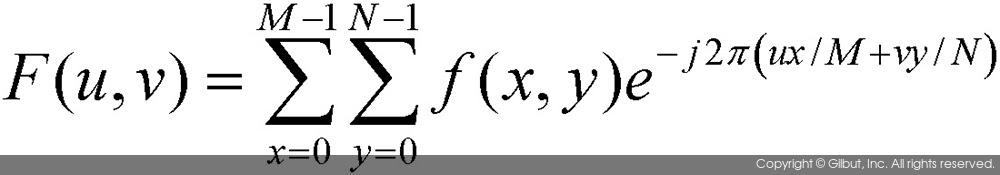
위 식에서 f(x, y)는 입력 영상을 나타내며, M은 영상의 가로 방향의 픽셀 개수이고, N은 세로 방향의 픽셀 개수이다. 2차원 영상에 대한 푸리에 변환 결과 함수 f(u, v)도 복소수 값을 갖는 복소 함수이다. 주파수 공간의 복소 함수 f(u, v)는 다음과 같은 이산 푸리에 역변환 공식에 의해 다시 원본 영상으로 변환될 수 있다.

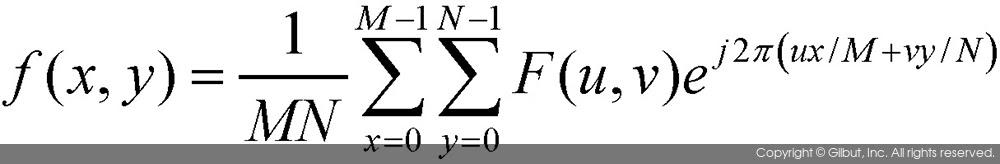
2차원 영상의 푸리에 변환 결과도 복소수로 표현되기 때문에 다음 수식과 같이 복소수의 절댓값의 크기와 위상으로 분할하여 표현할 수 있다.

F(u,v)=|F(u,v)|e^jφ(u,v)|

위 식에서 푸리에 변환 함수의 절댓값 |F(u, v)|는 다음과 같이 정의되며, 푸리에 스펙트럼^{Fourier spectrum}이라고도 불린다.

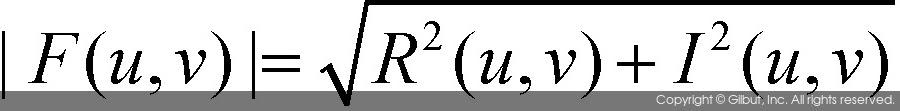
푸리에 변환 함수의 위상각^{phase angle}을 나타내는 함수 φ(u, v)는 다음 수식으로 정의된다.

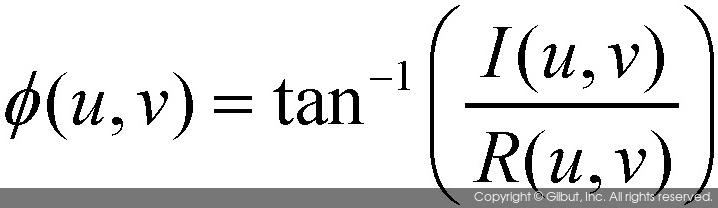
앞의 두 정의식에서 R(u, v)와 I(u, v)는 각각 F(u, v)의 실수부와 허수부를 나타낸다. 참고로 푸리에 스펙트럼을 제곱한 값을 파워 스펙트럼^{power spectrum}이라고 부르며, 수식은 다음과 같다.

P(u, v)=|F(u, v)|²
=R²(u, v)+I²(u, v)