10.2.3 개선된 2차원 영상의 푸리에 변환

앞에서 살펴본 DFT 함수는 정확한 푸리에 변환을 수행한다. 즉, 푸리에 변환 공식을 완벽하게 C/C++ 코드로 구현한 것이다. 그러나 이 코드를 사용하는 데에는 치명적인 문제점이 있다. 소스 10-4의 코드는 4중 for 루프를 사용하고 있고, 다수의 곱셈 연산을 호출하기 때문에 연산 속도가 매우 느리다. 만약 256×256 크기의 영상에 대하여 위 DFT 함수를 호출한다면, 아마 잠시 밖에 나가서 커피를 한 잔 마시고 와도 결과를 보기 힘들지 모른다.

가로 픽셀의 크기가 M이고, 세로 픽셀의 크기가 N인 영상을 일반적인 이산 푸리에 변환 공식을 사용하여 주파수 공간으로 변환할 때에는 N²M²개의 곱셈 연산이 필요하다. 그러므로 일반적인 이산 푸리에 변환 연산의 계산 복잡도는 O(kN⁴)로 표현된다. 이는 크기가 64×64인 영상을 DFT 함수를 사용하여 이산 푸리에 변환할 때 시간이 2초 걸렸다면, 256×256 크기의 영상을 이산 푸리에 변환할 때는 512초, 즉 8분이 넘게 걸린다는 소리이다. 영상의 한 변의 길이가 4배 증가하면, 전체 연산에 걸리는 시간은 4⁴=256배 증가하는 것이다.

다행히도 이산 푸리에 변환식은 행^row과 열^column 단위로 그 식을 분리하여 쓸 수 있다. 다음 수식을 살펴보자.

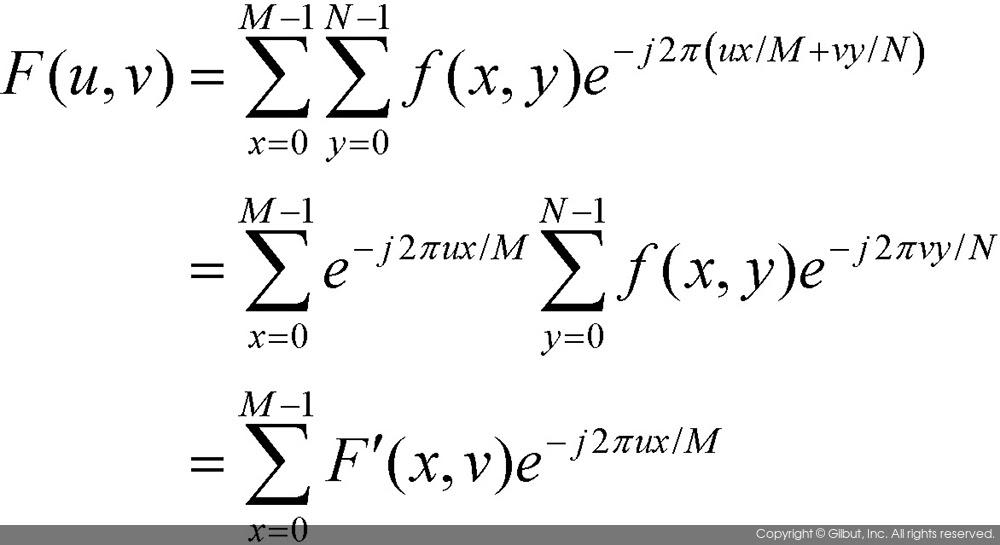
위 수식에서 함수 F´(x, v)는 다음과 같이 정의된다.

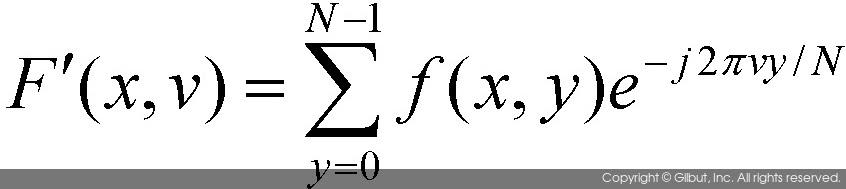
즉, 함수 F´(x, v)는 2차원 입력 영상에서 x번째에 해당하는 열을 1차원 데이터로 간주하여 이산 푸리에 변환을 수행함을 의미한다. 결국 2차원 영상의 푸리에 변환은 영상을 행과 열로 분리하여 각각을 푸리에 변환하여 구할 수 있음을 의미하는 것이다. 이 경우 행 단위로 먼저 1차원 푸리에 변환을 한 후 나중에 열 단위로 푸리에 변환을 수행하여도 결과는 동일하다.

이러한 영상의 푸리에 변환 과정을 그림 10-5에 나타내었다. 그림 10-5에서 왼쪽 입력 영상 f(x, y)를 각 행 단위로 분리하여 표시하였으며, 각 행을 푸리에 변환한 결과가 중앙의 F´(u, y)가 된다. 함수 F´(u, y)는 다시 열 단위로 분리되어 다시 1차원 푸리에 변환을 거치면 최종적으로 주파수 공간의 함수 F(u, v)로 변환된다.

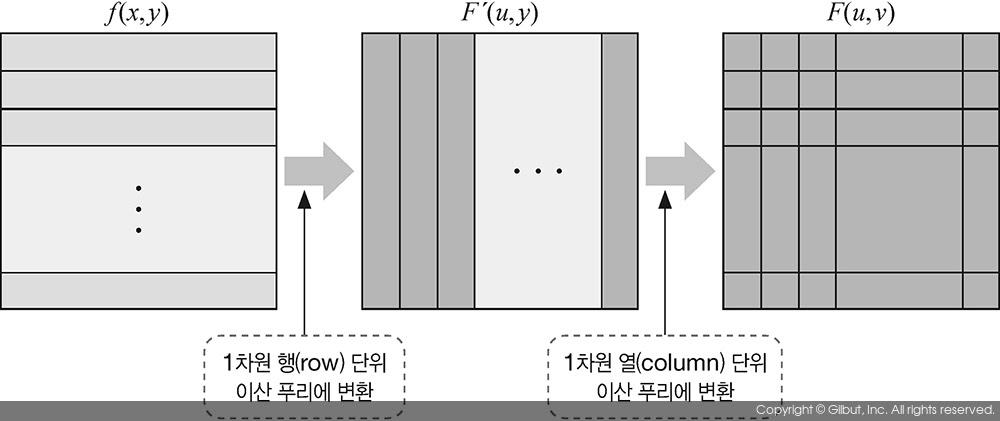
이처럼 2차원 영상을 이산 푸리에 변환을 할 때, 행과 열을 분리하여 이산 푸리에 변환을 수행하면 연산량이 상당히 감소하게 된다. 크기가 M×N인 영상을 행 단위 이산 푸리에 변환을 할 때, N번의 1차원 이산 푸리에 변환을 수행하므로 M²N번의 곱셈 연산이 필요하다. 그리고 열 단위 이산 푸리에 변환을 할 때는 MN²번의 곱셈 연산이 필요하다. 그러므로 행과 열을 분리하여 이산 푸리에 변환을 할 때에는 전체 MN(M+N)번의 곱셈 연산이 필요하게 된다. 이를 계산 복잡도로 표현하면 O(kN³)으로 나타낼 수 있다. 이는 앞서 살펴본 일반적 정의식에 의한 방법이 O(kN⁴)이었던 것에 비하면 연산 시간이 크게 감소함을 의미한다.