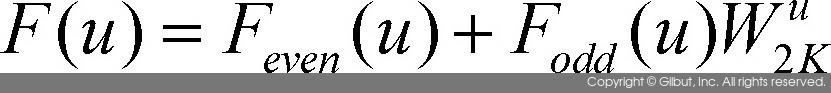10.3.1 고속 푸리에 변환의 이론적 배경
DFT 계산식에서 반복되는 연산을 최소화함으로써 푸리에 변환 계산 속도를 향상시키는 알고리즘을 고속 푸리에 변환Fast Fourier Transform이라고 하며, 영어 약자로는 FFT라고 쓴다. 고속 푸리에 변환 알고리즘은 원래 1차원 데이터에 대하여 정의된 알고리즘이며, 입력 데이터의 개수가 2의 승수로 이루어질 때에만 적용이 가능하다. 즉, N=2n으로 표현 가능할 때에만 사용할 수 있는 알고리즘이다.
고속 이산 푸리에 변환 알고리즘을 설명하기 위하여 1차원 데이터에 대한 이산 푸리에 변환식을 아래와 같이 조금 변형하여 다시 써보았다.
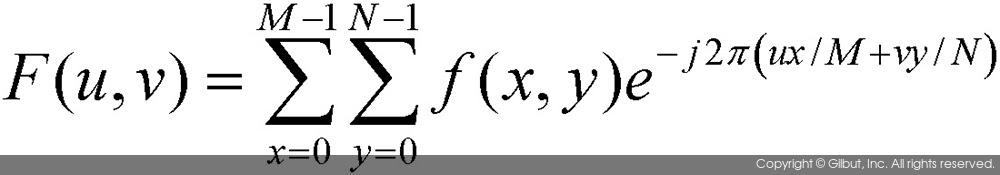
위 식에서 새로 나타난 기호 WN은 다음과 같이 정의하였다.
WN=e-j2π/N
앞에서 데이터의 개수를 나타내는 N이 2의 승수라고 정의하였기 때문에, N은 다음과 같이 다시 쓸 수 있다.
N=2K
위 식에서 K는 양의 정수이다. 기본적으로 고속 이산 푸리에 변환은 짝수 번째 데이터와 홀수 번째 데이터를 따로 분리하여 계산하는 방식이다. 그러므로 이산 푸리에 변환식을 짝수 번째 데이터와 홀수 번째 데이터로 분리하여 식을 정리하면 다음과 같이 쓸 수 있다.
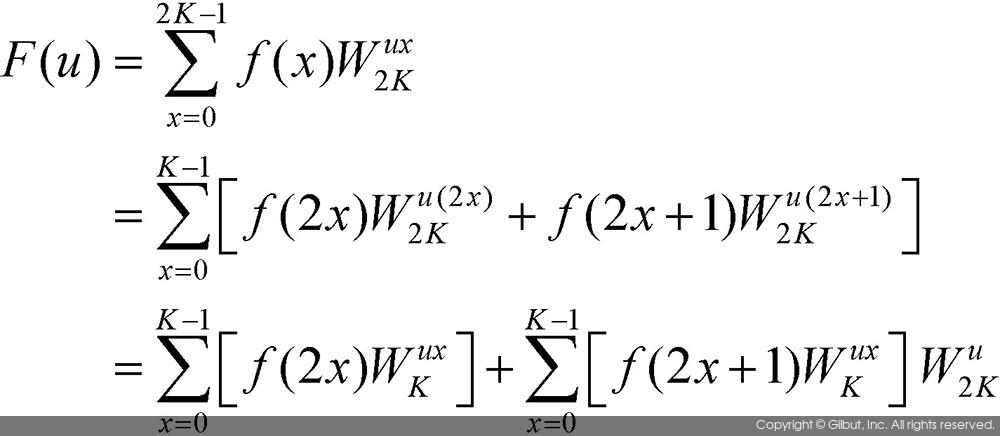
위 식에서 각각의 항을 다음과 같이 새로운 함수의 형태로 정의하자.
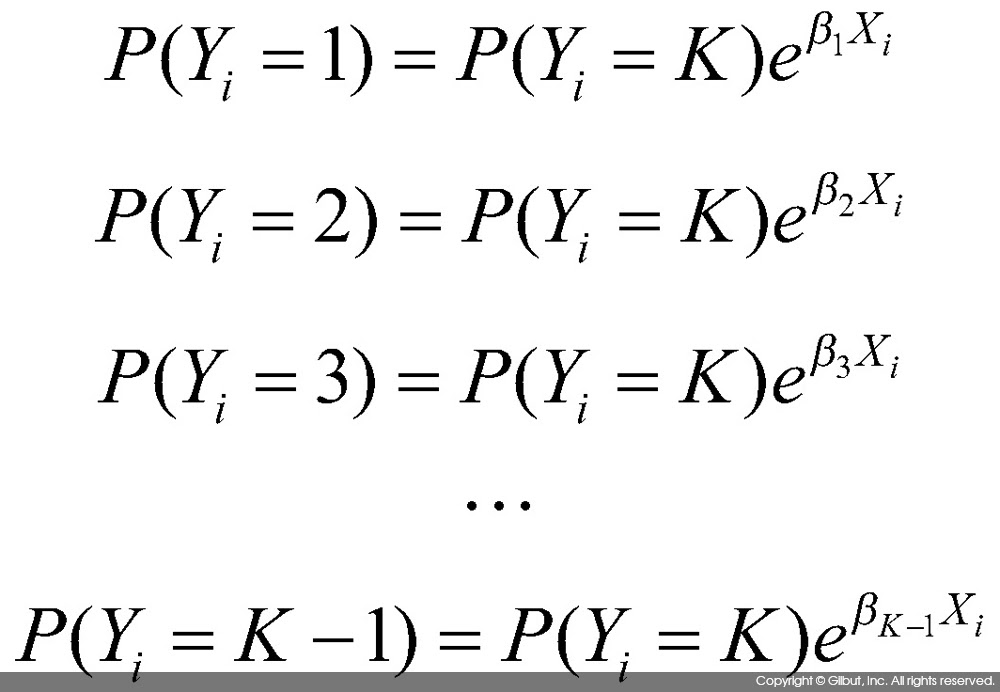
위 식에서 Feven(u) 함수는 입력 데이터의 짝수 번째 데이터만을 이용하여 푸리에 변환을 수행한 결과이며, Fodd(u) 함수는 홀수 번째 데이터만을 이용하여 푸리에 변환을 수행한 결과이다. 그러면 이산 푸리에 변환식은 다음과 같이 정리될 수 있다.