이제 흥미로운 결과를 도출해보자. 먼저 다음과 같은 두 수식을 살펴보자. W_N = e^-j2π|N임을 명심하고, u 대신에 u+K를 넣어서 식을 전개하면 다음 식이 만족된다.

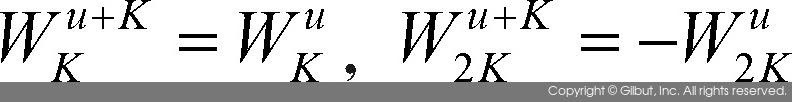
그러므로 F_even(u+K) = F_even(u)와 F_odd(u+K) = F_odd(u) 를 만족한다. 원래 F(u) 값은 u = 0, 1,..., 2K-1일 때 정의되는 값이다. 만약 u = 0,...,K -1일 때의 F(u) 값을 F_even(u)와 F_odd를 이용하여 구할 수 있다면, u = K,...,2K -1에서의 F(u) 값은 다음과 같은 수식을 이용하여 쉽게 구할 수 있다.

이것이 고속 푸리에 변환의 핵심 이론이다. N=2K개의 데이터를 이산 푸리에 변환을 할 경우, 짝수 번째 데이터들과 홀수 번째 데이터들을 이용하여 K개의 푸리에 변환 결과를 얻으면, 나머지 K개의 푸리에 변환 결과는 복잡한 연산 없이 쉽게 구할 수 있는 것이다.

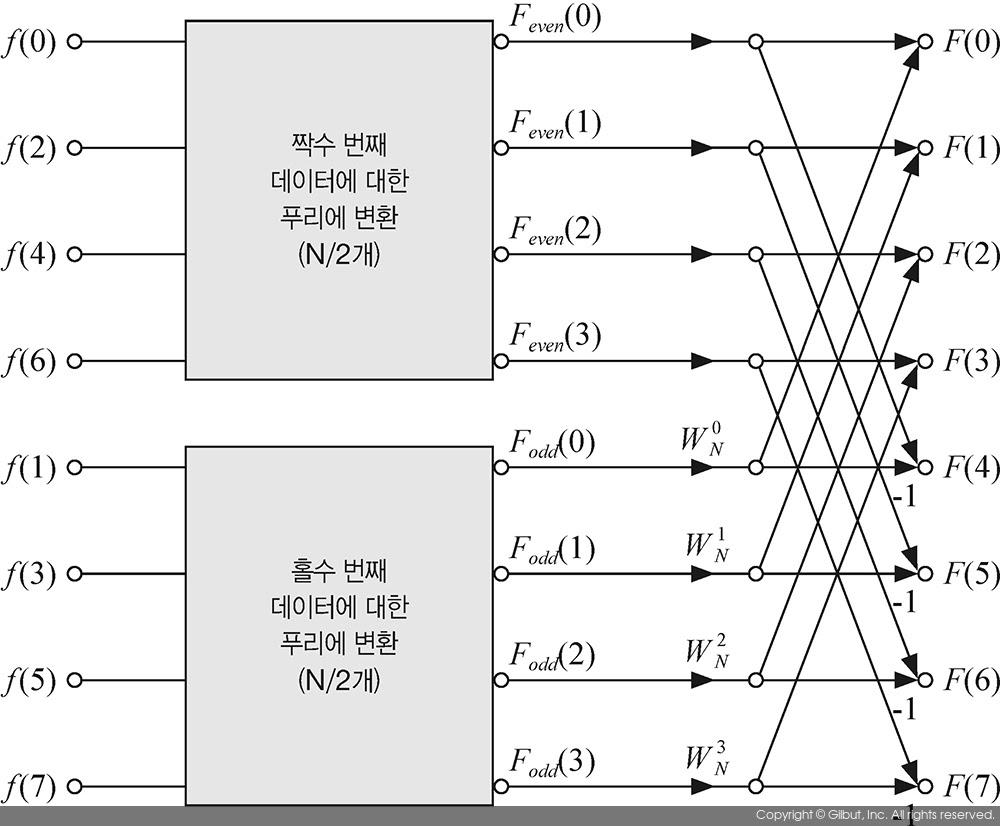
그림 10-9는 8개 데이터에 대하여 고속 푸리에 변환을 수행하는 방법을 보여준다. 좌측의 입력 데이터가 짝수 번째 데이터와 홀수 번째 데이터로 분리되어 나열된 것을 볼 수 있다. 그리고 4개의 짝수 번째 데이터를 이용하여 이산 푸리에 변환을 한 결과를 F_even(u)에 저장하고, 나머지 4개의 홀수 번째 데이터를 이용한 이산 푸리에 변환 결과를 F_odd(u)에 저장하였다. 최종적으로는 F_even(u)와 F_odd(u) 값을 이용하여 간단하게 F(u)를 계산하고 있다. 그림 10-9에서 오른쪽에 서로 엇갈리게 그려진 화살표의 상하에 쓰여진 수식 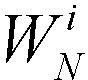또는 (-1)은 그 값을 곱해주라는 의미이다. 예를 들어 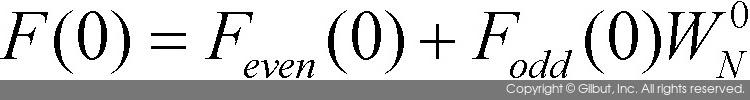으로 계산되고, 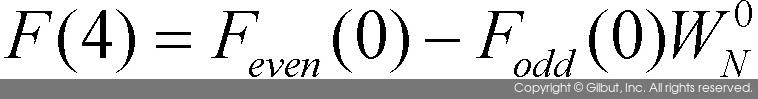형태로 계산된다. 그림 10-9의 오른쪽에 엇갈리게 그려진 화살표가 마치 나비의 날개와 비슷하다고 하여 이러한 연산 방법을 버터플라이^butterfly 방법이라고도 부른다.

고속 푸리에 변환 알고리즘이 진정으로 큰 의미를 갖는 이유는 버터플라이 연산 방법이 재귀적으로 수행될 수 있기 때문이다. 그림 10-9에서 8개의 입력 데이터를 홀수 번째와 짝수 번째의 데이터로 4개씩 나누어 이산 푸리에 변환을 수행하여 곱셈 연산의 횟수를 줄일 수 있었다. 이때 4개의 짝수 번째 데이터들을 이산 푸리에 변환한 결과를 F_even(u)로 정의하였는데, F_even(u)를 계산할 때에도 버터플라이 방법을 적용하여 곱셈 연산의 횟수를 줄일 수 있다. 즉, 고속 푸리에 변환 알고리즘은 최종적으로 입력 데이터가 1개가 될 때까지 버퍼플라이 방법을 사용하여 연산 횟수를 줄일 수 있다.