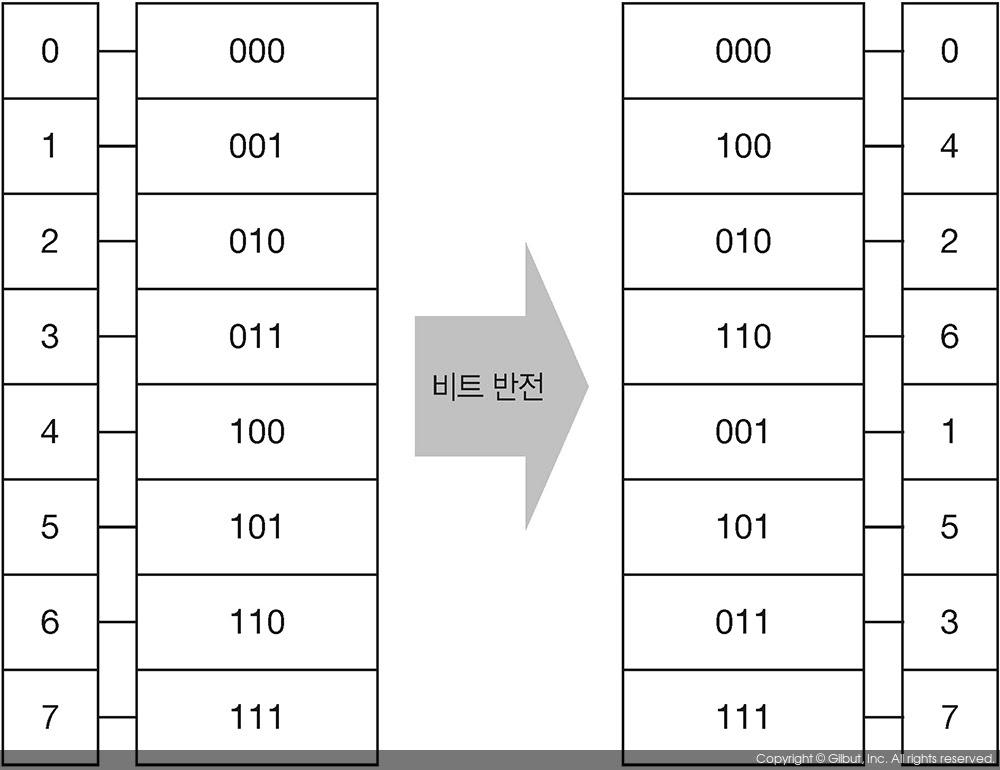
입력 데이터의 순서를 바꾸는 작업은 전통적으로 비트 반전^{bit reverse} 방법을 사용한다. 8개의 데이터의 순서는 이진수로 표현할 때 3개의 비트^bit를 이용하여 표현할 수 있다. 이들 비트의 앞뒤 순서를 반전하는 것을 비트 반전이라고 한다. 그림 10-12는 비트 반전으로 8개 데이터의 순서를 변경한 예를 보여준다. 각 데이터의 순서는 0을 기반으로 표현함을 기억하기 바란다. 예를 들어 입력 데이터의 인덱스^index가 1인 경우, 이를 이진수로 표현하면 001₍₂₎이 된다. 이것을 비트 반전을 거치면 100₍₂₎이 되고, 이는 십진수로 4의 값을 갖는다. 그러므로 f(1)에 위치해 있던 데이터를 f(4)의 위치로 이동해주어야 한다. 나머지 데이터들도 마찬가지의 연산을 수행한다. 만약 입력 데이터의 개수가 16=2⁴개인 경우에는 4개의 비트에 대하여 비트 반전을 수행한다.

N개의 데이터를 고속 푸리에 변환 알고리즘을 이용하여 주파수 공간으로 변환할 때 드는 계산량에 대하여 알아보자. 일반적인 이산 푸리에 변환은 앞에서 N²번의 곱셈이 필요하다고 설명하였다. 고속 푸리에 변환에서는 계산 단계가 log₂N으로 줄어들고, 각 단계에서는 N번의 곱셈과 덧셈이 필요하다. 그러므로 고속 푸리에 변환 알고리즘의 계산 복잡도는 O(Nlog₂N)으로 표현한다.

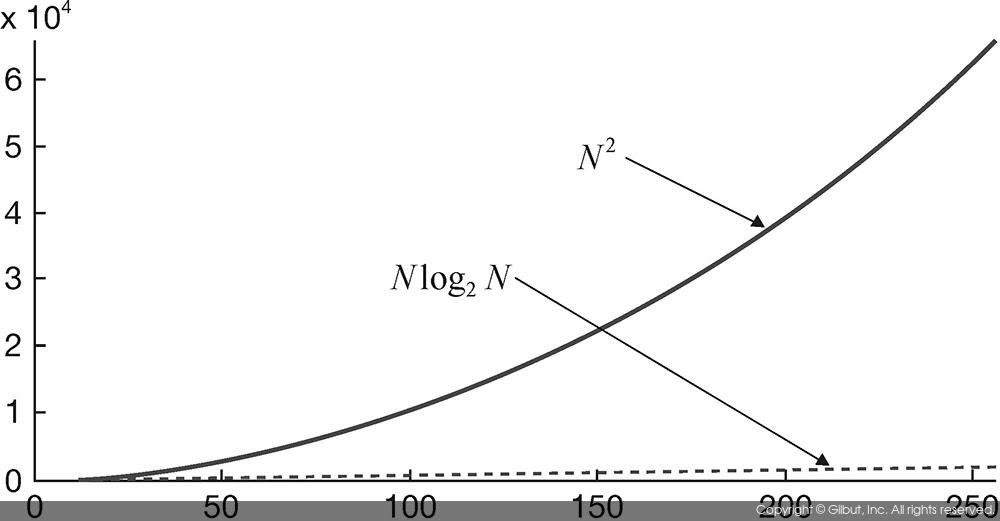
그림 10-13은 데이터의 개수가 1~256까지 변화할 때, 일반 이산 푸리에 변환(DFT)과 고속 푸리에 변환(FFT)에 필요한 연산량을 그래프의 형태로 나타낸 것이다. DFT 연산량을 나타내는 N² 그래프가 급격하게 증가하는데 비하여, FFT 연산량을 나타내는 Nlog₂N 그래프는 상대적으로 완만한 증가를 보여주고 있다. FFT 알고리즘을 사용하였을 때의 연산량의 감소 이득은 데이터의 개수 가 증가할수록 더욱 유리하게 작용한다.