일반적으로 영상의 엣지에서는 그레이스케일 값이 급격하게 변화하기 때문에 영상의 미분 값 또한 크게 나타난다. 그러므로 영상의 미분 함수를 구하고, 그 값이 크게 나타나는 위치를 엣지 위치로 간주할 수 있다.

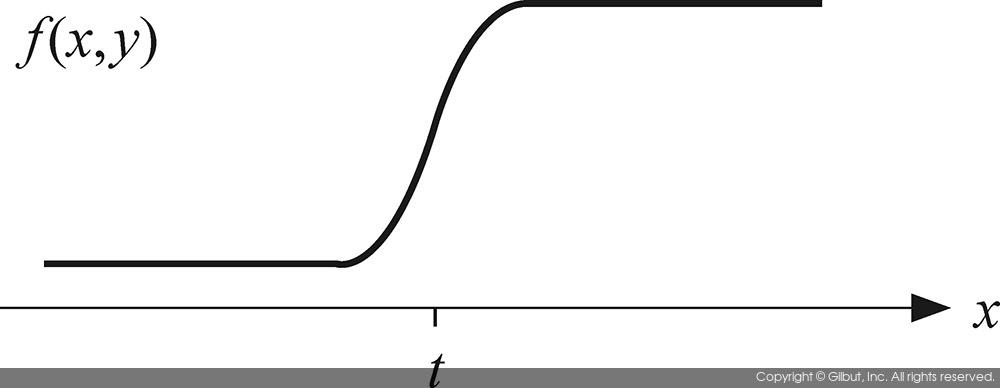
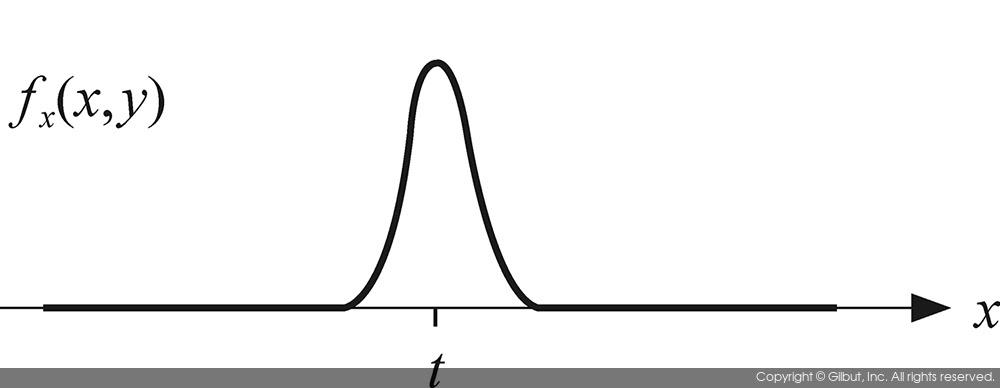
그림 11-2는 연속 함수 f(x, y)에 대하여 엣지에서의 미분 값을 보여준다. 이 그림에서 y 값은 고정되어 있고, x 값의 변화에 따른 f(x, y)의 변화만을 보여주고 있다. 그림 11-2(a)는 입력 함수의 모습을 보여주며, x=t 부근에서 값이 급격하게 증가하는 것을 볼 수 있다. 이러한 함숫값의 변화는 영상의 엣지 부근에서 나타나는 현상이며, 실제 영상에서는 x 값이 증가함에 따라 밝기가 급격하게 증가하는 현상으로 나타난다. 함수 f(x, y)의 x축 방향으로의 1차 미분을 그래프로 나타낸 것이 그림 11-2(b)이다. 함수 f_x(x, y)의 값은 x=t 부근에서만 큰 값을 갖고, 나머지 부분에서는 거의 0 값을 갖는다. 그러므로 영상에서 엣지를 검출하기 위해서는 영상을 미분한 후, 미분 값이 특정 임계값^threshold보다 큰 부분을 찾으면 된다.

그러나 미분은 기본적으로 연속 함수에 대해 정의된 수학적 개념이다. 이를 이산 함수에 해당하는 영상에 적용하기 위해서는 미분 함수를 근사화하여 사용해야 한다. 일반적으로 다음의 세 가지 미분 근사^{approximation} 방법이 사용되고 있다.

• 순방향 차이^{Forward difference}:

• 역방향 차이^{Backward difference}: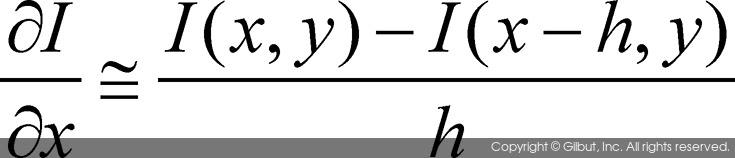

• 중간값 차이^{Centered difference}: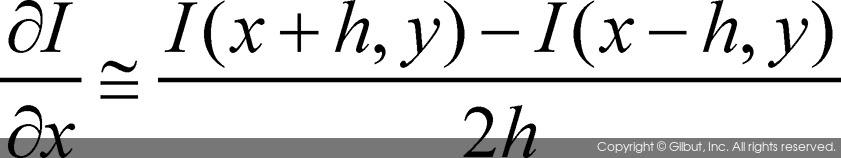

위 수식에서 I(x, y)는 영상과 같은 2차원 이산 함수를 나타내고, h는 이산값의 간격을 의미한다. 미분 근사 방법을 영상에 적용할 경우, h는 픽셀의 간격을 의미하며 1로 간주할 수 있다. 위 세 가지 미분 근사 방법 중에서 중간값 차이를 이용하는 방법이 이론적으로 근사화 오류가 가장 적기 때문에 널리 사용되고 있다. 중간값 차이 방법을 마스크 연산의 형태로 변환하면 그림 11-3과 같이 나타낼 수 있다.