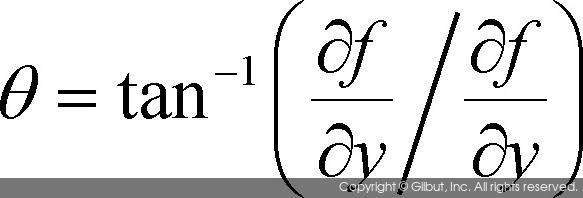영상은 2차원 공간에서 정의된 함수이기 때문에, 영상에서 미분 값을 이용하여 엣지를 찾기 위해서는 가로 방향과 세로 방향의 미분 값을 함께 사용해야 한다. 2차원 공간상에서의 함수 f(x, y)가 있을 때, 이 함수의 그래디언트^gradient는 다음과 같이 벡터 형태로 정의된다.

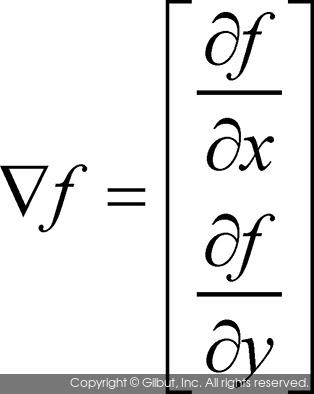
2차원 함수의 그래디언트는 위 수식과 같이 함수 f(x, y)를 x축과 y축으로 각각 편미분^{partial derivative}하여 벡터 형태로 표현한 것이다. 그래디언트가 벡터이기 때문에 그래디언트는 크기와 방향 성분으로 표현할 수 있다. 그래디언트 벡터의 방향이 변화의 정도가 가장 심한 방향이고, 그래디언트 벡터의 크기는 변화의 정도를 나타내는 척도로 생각할 수 있다. 다음은 그래디언트의 크기를 구하는 수식이다.

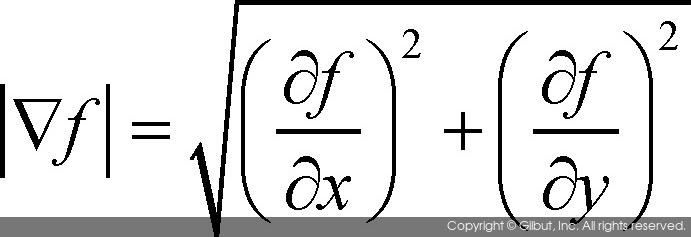
영상에서 엣지 위치를 찾기 위해서는 위와 같은 그래디언트의 절댓값을 계산하고, 이 값이 특정 값보다 큰 경우에 한하여 엣지로 정의한다. 여기서 엣지 여부를 판단하기 위해 기준이 되는 값을 문턱치 또는 임계값^threshold이라고 부른다. 위 수식과 중간값 차이에 의한 미분 함수의 근사를 동시에 사용하여 수식을 작성하면 다음과 같은 엣지 검출 조건을 얻을 수 있다.

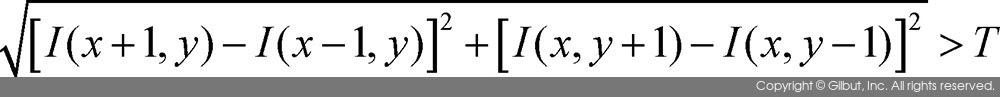
즉, 좌표 (x, y)에서 위 수식을 만족한다면 점 (x, y)는 엣지로 간주할 수 있다. 위 수식에서 T는 임계값을 의미한다.

참고로 구현의 편의를 위하여 그래디언트 크기를 다음과 같이 근사화하기도 한다. 이 경우 곱셈 과 제곱근 연산이 없어지므로 구현이 빠르고 간단해진다.

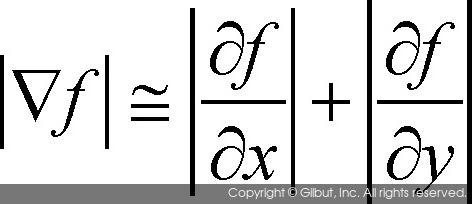
또한 그래디언트 벡터가 가리키는 방향, 즉 가장 경사가 심한 방향은 다음과 같이 삼각 함수를 사용하여 구할 수 있다.