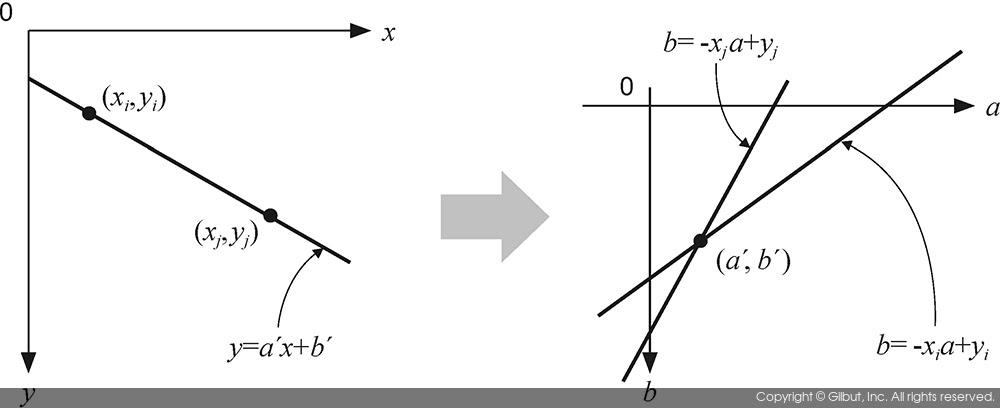
그림 11-15는 xy 좌표 공간을 ab 좌표 공간으로 변환하는 방법을 보여준다. 그림 11-15(a)에 나타난 직선의 방정식은 임의의 두 점 (x_i, y_i)와 (x_j, y_j)를 지나고 있다. 이 직선이 점 (x_i, y_i)를 지나가기 때문에, y_i=ax_i+b의 식을 만족하며, 이를 ab 공간으로 변형하면 b=-x_ia+y_i로 쓸 수 있다. 여기서 x_i와 y_i는 상수이므로 ab 공간에서 정의된 b=-x_ia+y_i는 직선의 방정식이 된다. 마찬가지로 점 (x_j, y_j)는 그림 11-15(b)에서 b=-x_ja+y_j 형태의 직선을 결정한다. 이 두 직선이 서로 교차하는 점의 좌표는 (a´, b´)가 되며, 이는 xy 공간에서 직선의 방정식 y=a´x+b´를 정의해주는 두 개의 파라미터 값이다.

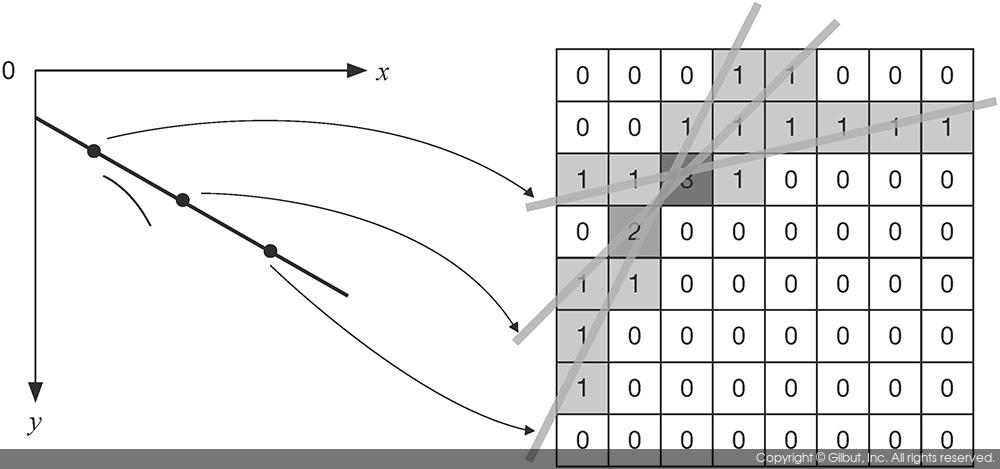
그러므로 허프 변환을 이용하여 직선의 방정식을 찾기 위해서는 xy 공간에서 엣지로 판명된 모든 점의 좌표를 ab 파라미터 공간으로 변경하여 직선을 그려주고, 직선들이 많이 교차되는 점을 찾으면 된다. 이때 직선이 교차하는 점을 찾기 위해서 보통 축적 배열^{accumulation array}을 사용한다. 축적 배열이란 일반적인 2차원 배열의 형태이며, 직선이 지나가는 위치의 배열 원소의 값을 1씩 증가시킨다. 그림 11-16은 이러한 축적 배열을 만드는 방법의 예를 보여준다. 왼쪽의 2차원 xy 영상 좌표계에 있는 3개의 점을 이용하여 ab 파라미터 공간에서 3개의 직선을 오른쪽 배열 위에 그려보았다. 그리고 직선이 지나가는 배열 좌표의 값을 1씩 증가시켰다. 그림 11-16의 예에서는 3개의 직선이 공통으로 지나간 위치의 값이 3이 되어 최댓값을 가지게 됨을 볼 수 있다. 영상 좌표계에 있는 모든 엣지 픽셀에 대하여 이러한 작업을 수행한 후, 최종적으로 축적 배열에서 최댓값이 존재하는 위치를 찾아 그 위치에서 배열의 인덱스^index에 해당하는 a´, b´를 찾으면 원래 직선의 방정식의 파라미터 값을 구할 수 있다.