한 가지 문제점은 위에서 사용한 직선의 방정식 y=ax+b는 y축과 평행한 직선을 표현하지 못한다는 점이다. 왜냐하면 수직선의 경우 기울기 a 값이 무한대의 값을 가지기 때문이다. 그러므로 실제 허프 변환을 구현할 때에는 다음과 같이 극좌표계 형태로 직선의 방정식을 사용한다.
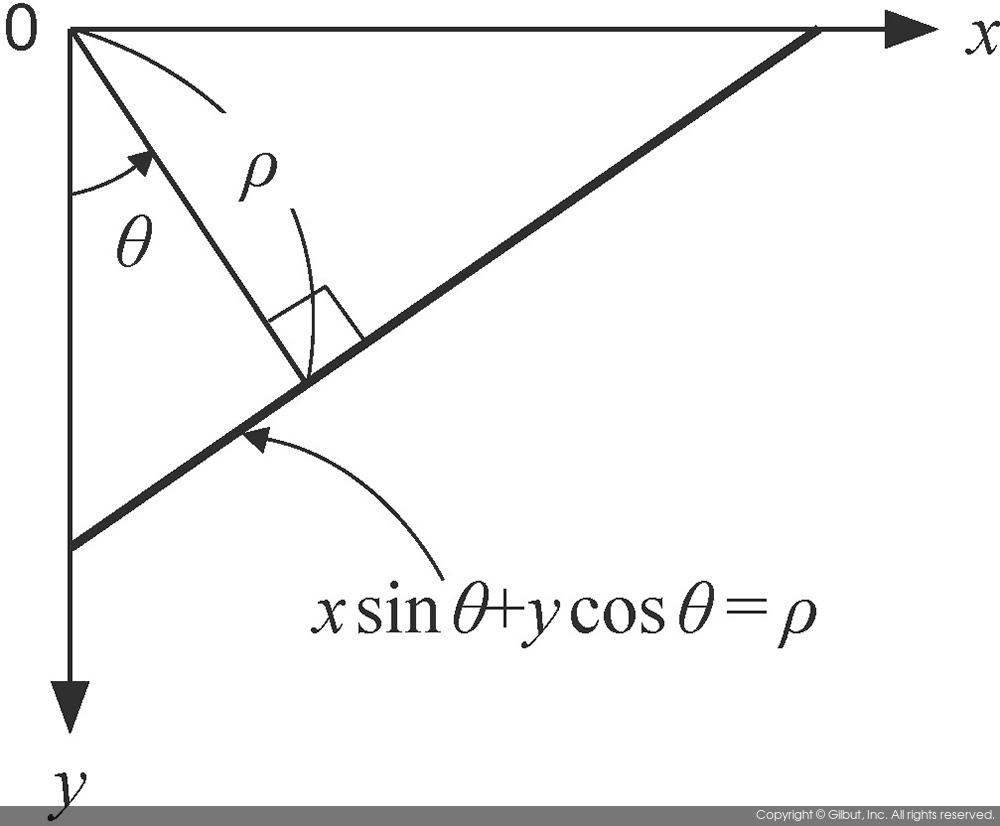
xsinθ+ycosθ = ρ
위 수식에 해당하는 직선의 모양을 그림 11-17에 나타내었다. 위 수식에서 ρ는 원점 (0, 0)에서 직선까지의 수직 거리를 의미하고, θ는 원점에서 직선에 수직선을 그렸을 때 y축과 이루는 각도의 크기를 의미한다.
이처럼 직선을 ρθ 파라미터 공간에서 표현할 경우, ρ와 θ가 가질 수 있는 값의 범위는 다음과 같다.
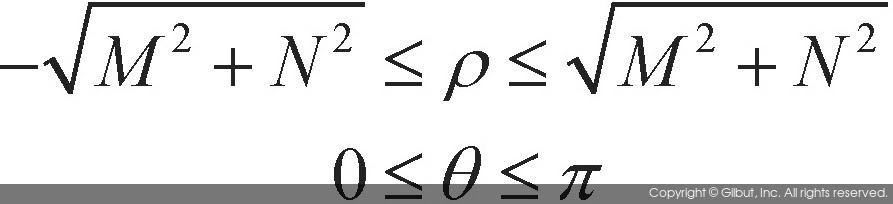
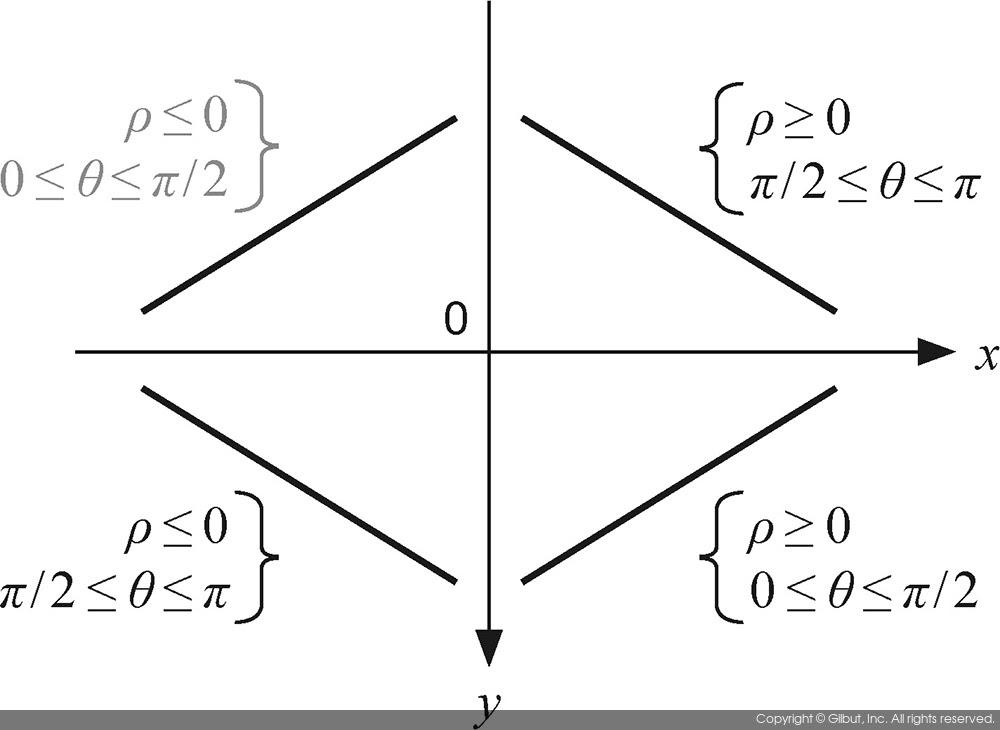
위 수식에서 M과 N은 영상의 가로와 세로 픽셀의 크기를 의미한다. 직선의 방향에 따라 ρ 값은 음수를 가질 수 있다. 영상의 xy 좌표 공간에서 실제 직선의 모양에 따른 ρ와 θ의 값의 범위를 그림 11-18에 나타내었다. 즉, 원점에서 직선에 내리는 수직 선분의 방향이 x축을 기준으로 음수 방향으로 향할 때 ρ 값은 음수를 갖는다. 그림 11-18에서 x와 y가 모두 음수인 사분면에서의 직선은 실제 영상에서는 존재할 수 없는 형태의 직선이므로 파라미터 값의 범위를 회색으로 표현하였다.
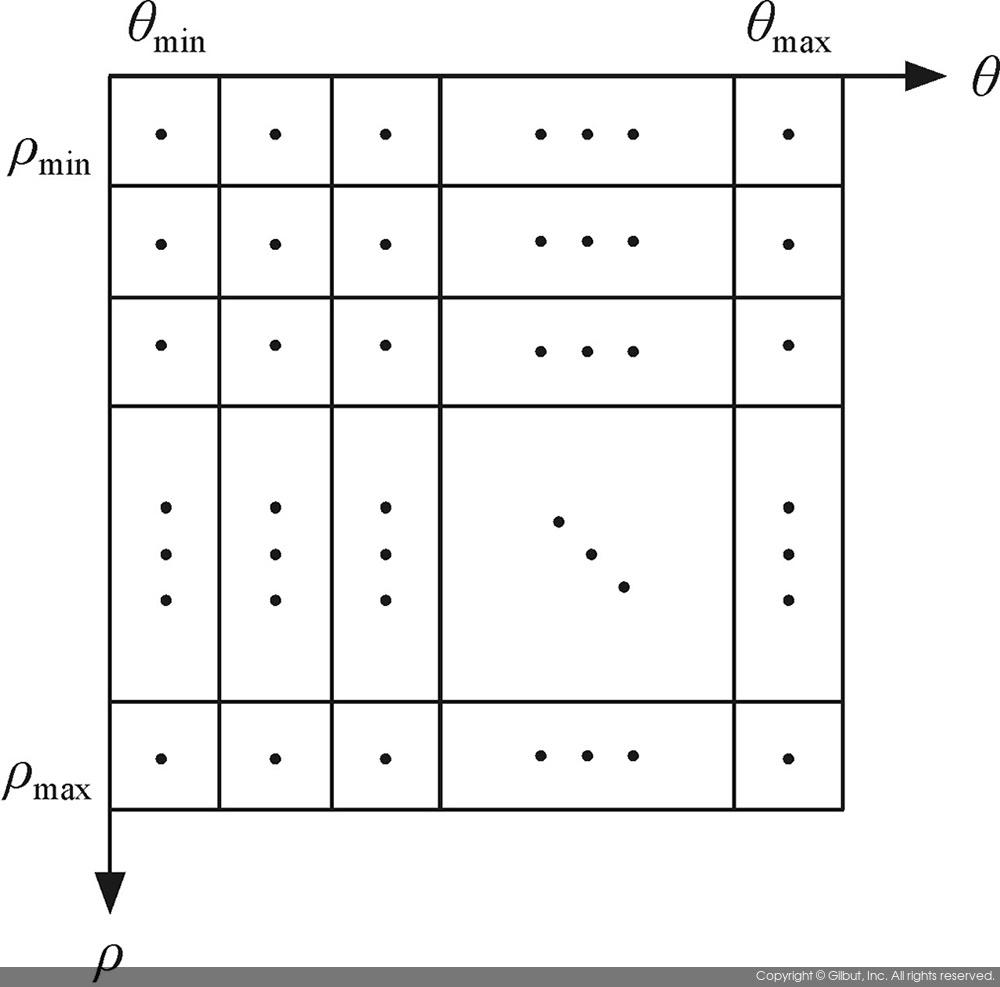
이처럼 ρθ 파라미터 공간을 사용하는 허프 변환을 구현할 때에도 축적 배열을 사용한다. 그림 11-19는 ρθ 파라미터 공간에서 축적 배열의 구성을 보여준다. 이 책에서는 2차원 배열의 각 행에 ρ 값을 지정하고, 각 열에는 θ 값을 지정하도록 구현하였다. 실제 ρ와 θ는 실숫값을 가지기 때문에 그림 11-19와 같은 축적 배열을 C/C++ 코드로 구현하려면 실숫값을 적당한 크기로 나누어 저장하는 양자화quantization 과정을 거쳐야 한다. 이에 대한 좀 더 자세한 내용은 나중에 허프 변환의 구현 부분에서 다시 다루도록 하겠다.