그러면 해리스 코너 검출 알고리즘을 수식적으로 분석해보자. 먼저 그림 11-22에서 살펴본 것과 같이 특정 윈도우를 이용하여 주변 픽셀과의 차이를 구하는 수식은 다음과 같다.

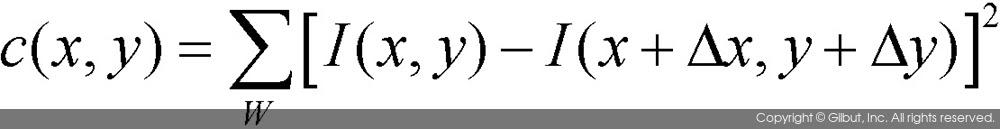
위 식에서 Δx와 Δy는 x와 y 방향으로의 작은 변화량을 의미하고, W는 윈도우를 의미한다. 즉, Δx와 Δy는 W로 정의된 윈도우 내에서의 변화량이다 이때 윈도우 W는 보통 가우시안 형태의 가중치를 반영하도록 만들어진다. 변화량을 나타내는 함수 c(x, y)의 값은 평탄한 영역에서는 그 값이 작게 나타나고, 코너 위치에서는 값이 크게 나타날 것을 예상할 수 있다. 위 수식에서 (Δx,Δy)만큼 이동된 위치에서의 픽셀 값 I (x + Δx, y + Δy)는 테일러 급수^{Taylor series}에 의해 다음과 같이 근사될 수 있다.

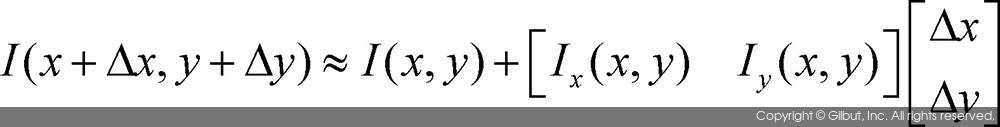
이 식을 c(x, y)를 정의한 첫 번째 수식에 대입하여 정리하면 다음과 같이 수식이 전개된다.

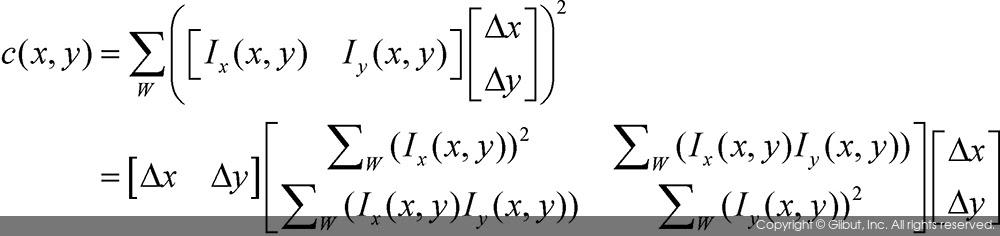
위 수식에서 중앙의 2×2 행렬을 M이라고 정의하도록 하자. 행렬 M은 다음과 같은 형태로 다시 작성할 수 있다.

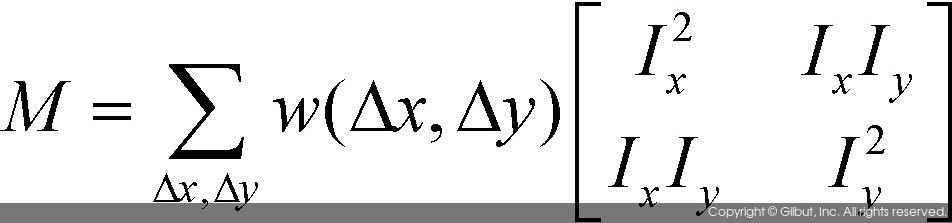
원래 함수 c(x, y)는 지역적 자기 상관 함수^{local autocorrelation function}와 관련이 있으며, 행렬 M은 이 함수의 모양을 결정하는 행렬이다. 만약 행렬 M의 고윳값^eigenvalue을 λ₁과 λ₂라고 표현한다면, λ₁과 λ₂의 값의 크기에 따라 해당 픽셀이 평탄한 영역인지 엣지, 혹은 코너 포인트 위치인지가 결정된다. 만약 λ₁과 λ₂가 모두 작은 값을 가지면 해당 점은 평탄한 영역에 속한 점으로 볼 수 있다. 만약 λ₁과 λ₂ 중 하나는 큰 값을 갖고, 다른 하나는 작은 값을 가지면 이는 엣지에 위치한 픽셀이다. 만약 λ₁과 λ₂ 모두 큰 값을 가지면 이는 코너 포인트에 위치한 픽셀일 가능성이 크다. λ₁과 λ₂의 값이 크다는 점은 그림 11-22와 같이 해당 좌표에서 윈도우를 씌워 주변과 픽셀 값을 비교하였을 때 모든 방향으로 큰 차이가 나타남을 의미하기 때문이다.

Note | 테일러 급수와 고윳값

테일러 급수란 함수의 특정 좌표에서 몇 번이고 미분이 가능할 때, 주변 좌표에서의 함숫값을 그 도함수를 이용하여 구하는 방법이다. 테일러 급수를 2차 차수까지 수식으로 표현하면 다음과 같다.

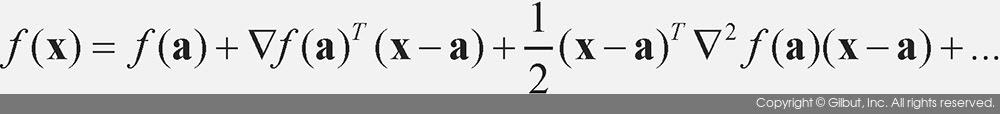
고윳값이란 행렬 A가 존재할 때, 수식 Aχ_i = λ_iχ_i를 만족하는 λ_i 값들을 의미한다. 이때 벡터 χ_i는 고유벡터(eigenvector)라고 부른다.

테일러 급수와 고윳값에 대한 자세한 설명은 이 책의 범위를 벗어나기 때문에, 좀 더 자세한 내용은 대학 수준의 수학 서적(해석학 및 선형 대수)을 참고하기 바란다.