해리스 코너 포인트 검출 방법에서는 행렬 M의 고윳값을 직접 구하는 방법 대신 코너 응답 함수corner response function를 새롭게 정의하여 이 값을 코너 포인트를 찾는 척도로 사용한다. 코너 응답 함수는 다음과 같이 정의하였다.
R = Det(M)-k⋅Tr(M)2
위 수식에서 Det(M)은 행렬 M의 행렬식determinant 값을 의미하고, Tr(M)은 행렬 M의 대각합(트레이스, trace)를 의미한다. 2×2 행렬 M에서 이 두 값은 고윳값 λ1, λ2에 대하여 다음과 같은 성질을 만족한다.
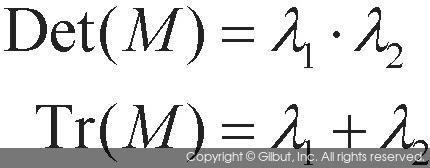
즉, 행렬의 고윳값을 직접 구하는 대신 행렬식과 대각합을 이용하여 고윳값의 곱과 합을 구하여 사용하겠다는 의미로 해석할 수 있다. 2×2 행렬에서 행렬식과 대각합을 구하는 방법은 다음 해리스 코너 검출기 구현 파트에서 설명하도록 하겠다. 코너 응답 함수 R의 값에 따라 평탄한 영역, 엣지 픽셀, 코너 픽셀을 구분하면 그림 11-23과 같이 구간을 분리할 수 있다. 일반적으로 코너 응답 함수에서 상수 k 값은 0.04~0.06 사이의 값을 주는 것이 좋다고 알려져 있다.
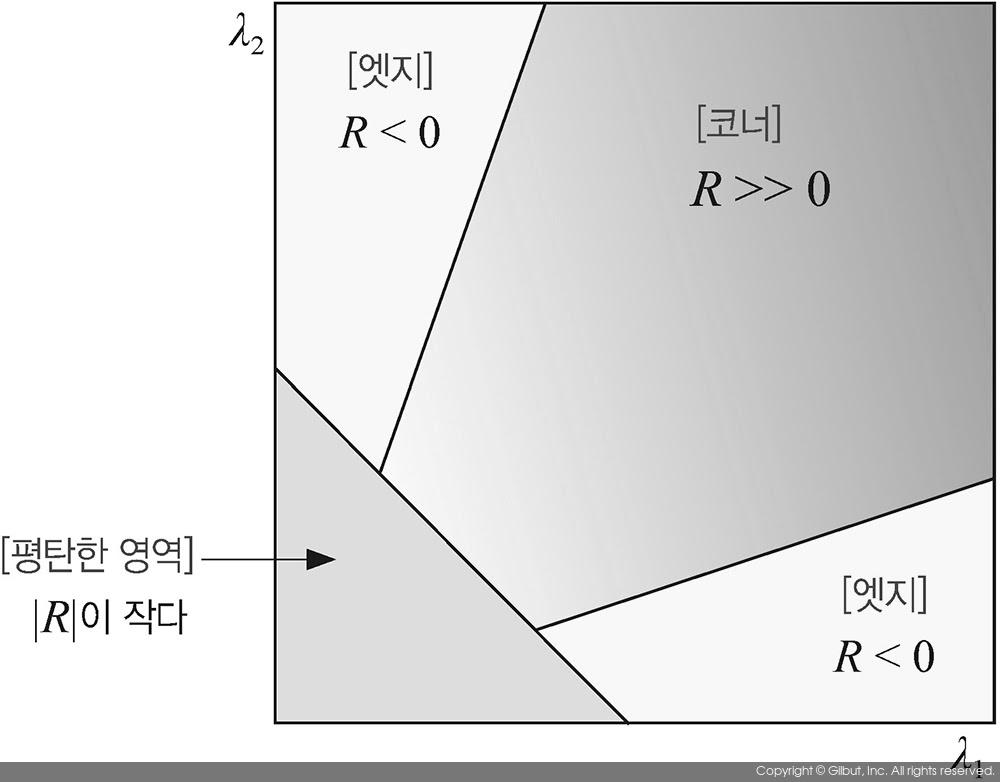
그림 11-24는 해리스 코너 검출 방법을 이용하여 실제 영상에서 코너 위치를 찾은 예를 보여준다. 그림 11-24(a)는 입력 영상인 polygon.bmp 파일이다. 이 영상에 대하여 코너 포인트를 찾은 결과를 그림 11-24(b)에 나타내었다. 비교적 단순한 형태의 영상이기 때문에 정확하게 코너 점의 위치를 찾아낸 것을 볼 수 있다. 그림 11-24(C) 그림은 입력 영상인 (a)를 30° 회전한 후, 영상의 크기를 양선형 보간법을 이용하여 256×256으로 줄인 영상이다. 이 영상에 대하여 코너 포인트를 찾은 결과를 그림 11-24(d)에 나타내었다. (b)에서 찾은 코너 포인트를 모두 동일하게 찾아낸 것을 볼 수 있다. 이처럼 해리스 코너 검출 방법은 회전과 어느 정도의 크기 변환에도 정확하게 코너 위치를 찾아내는 성질이 있기 때문에 많은 객체 인식 및 추적 분야에서 사용되고 있다.



