코사인 거리
유클리드 거리와 맨해튼 거리는 고차원 공간에서는 잘 동작하지 않는 단점이 있습니다. 고차원 공간에서 두 포인트 사이의 거리를 더 정확히 잴 수 있는 방법은 코사인(Cosine) 거리입니다. 코사인 거리는 원점에 연결된 두 포인트가 만들어내는 각도의 코사인 값을 계산하여 구합니다. 포인트들이 서로 가깝다면 이들이 만들어내는 각도가 작습니다. 이와 반대로, 서로 거리가 멀다면 그 각도도 커집니다.
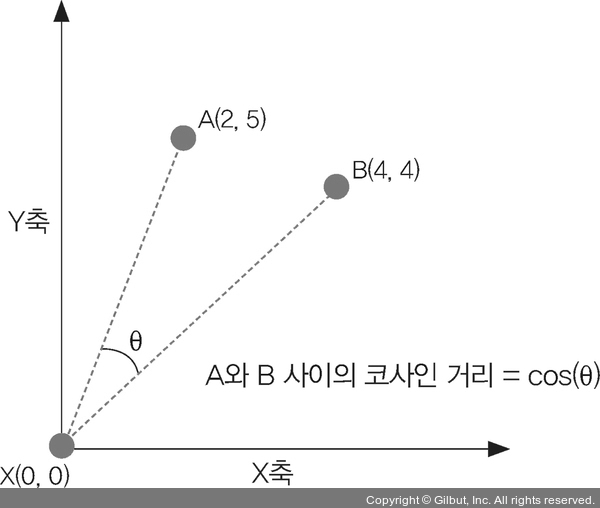
▲ 그림 6-7 A와 B 사이의 코사인 거리
주의 ≡
텍스트 데이터는 보통 고차원 공간상의 벡터로 표현됩니다. 코사인 거리는 고차원 공간에서 매우 잘 동작하기 때문에 텍스트 데이터에 적합합니다.
그림 6-7에서 두 포인트 A(2, 5)와 B(4, 4)가 만들어내는 각도의 코사인 값을 코사인 거리라고 설명했습니다. 이 두 포인트 사이에 위치한 포인트는 원점인 X(0, 0)입니다. 실제로는 원점이 아니어도 문제 공간상에 존재한다면 코사인 거리를 구하는 데 사용할 수 있습니다.