회귀 모델 평가하기

앞에서 그었던 직선은 종속 변수와 독립 변수 간의 관계를 근사한 것입니다. 최적의 직선도 실젯값에서 어느 정도 벗어나 있게 마련입니다.

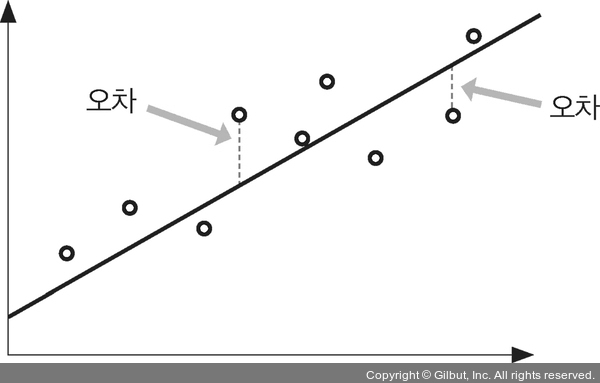
▲ 그림 7-10 회귀 직선과 오차

선형 회귀 모델의 성능을 정량화하는 전형적인 방법은 평균 제곱근 오차(Root Mean Square Error, RMSE)입니다. 이는 모델이 가진 오차의 표준 편차를 수학적으로 계산합니다. 훈련 데이터셋에 담긴 특정 사례의 손실 함수는 다음과 같습니다.

Loss(ý⁽ⁱ⁾, y⁽ⁱ⁾) = 1/2(ý⁽ⁱ⁾ - y⁽ⁱ⁾)²

비용 함수는 훈련 데이터셋 전체의 손실을 최소화합니다.

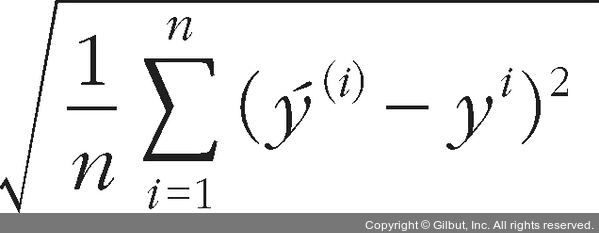
RMSE는 어떻게 해석해야 할까요? 만약 제품의 가격을 예측하는 모델의 RMSE가 $50라면, 이는 전체 예측의 68.2%가 실젯값의 $50(α) 내에 분포한다는 의미입니다. 또한, 이는 전체 예측의 95%가 실젯값의 $100(2α) 내에 분포하고, 마지막으로 99.7%의 예측값이 실젯값의 $150 내에 분포한다는 의미입니다.