제12장에 들어가자 마침내 사칙연산에서 벗어난 수학 개념이 나오기 시작했는데, 처음 소개된 개념은 수열이다. 레오나르도가 고대 이집트의 수학 또는 피타고라스 학파의 수학 이론도 공부했음을 짐작해 볼 수 있는 대목이다.

7, 10, 13, 16, 19, 22, 25, 28, 31

예를 들어 위와 같이 일정한 수 간격으로 증가하는 수열의 합을 구하는 방법을 레오나르도는 책에서 다음과 같이 제시하였다.

이에 따라 위 수열의 합을 계산하면 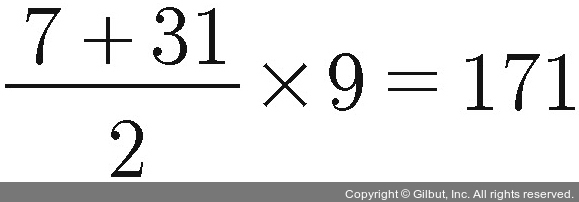이다. 이 수열의 합 공식은 내가 이아손이었던 시절에 피타고라스학파 수학 서적들에서도 보았던 거다.

몹시 의아한 건 이 책에는 이러한 합 공식이 왜 성립하는지를 설명하지 않았다는 점이다. 분명히 책의 서문에서는 증명을 기반으로 이론 중심의 책을 집필했다고 언급했으면서 말이다.

사실 제12장까지 읽으면서도 여태껏 내가 받은 이 책의 인상은 서론에서 말한 것과 같은 이론 중심의 책이라기보단 현실에의 적용을 중심으로 집필된 책이라는 쪽에 더 가깝다. 상당수의 증명을 건너뛰고서 이론의 결과와 그 사례를 보이는 데에 대부분의 분량을 할애하고 있었기 때문이다.