• O(logn): 크기가 커질수록 처리 시간이 짧아지는 알고리즘입니다. 아주 많은 데이터가 존재하더라도 매우 짧은 시간에 끝나기 때문에 이상적인 알고리즘이라고 할 수 있습니다. 이진 탐색이 가장 대표적이며, (정렬된) 배열에서 어떤 숫자를 찾을 때 찾아야 하는 숫자보다 작은 숫자 데이터들은 탐색하지 않으므로 탐색할 범위가 계속 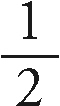씩 줄어듭니다. 꼭 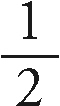이 아니더라도 비례해서 줄어든다면 해당 시간 복잡도에 속한다고 말할 수 있습니다.

• O(n): 입력 데이터 수만큼 정직하게 시간을 소모하는 알고리즘입니다. 배열 탐색이나 초기화, for 문 1개 사용, 문자열 탐색, 데이터 재구축 등 입력 데이터를 다루는 동작 대부분이 이에 해당합니다. 그래서 가장 경계해야 할 시간 복잡도이기도 합니다. O(n) 알고리즘이 두 번 중첩되도록 유도하는 문제에서 이 알고리즘을 사용하면 바로 시간 복잡도가 O(n²)이 되어 시간이 매우 길어지므로 항상 조심해서 사용해야 합니다.

• O(nlogn): 입력 데이터 수에 비례해서 연산이 추가로 필요한 알고리즘입니다. 정렬을 사용한다면 무조건 이 정도의 시간이 걸린다고 봐도 무방합니다. 주어진 데이터를 ‘정렬’하라는 문제라면 O(nlogn) 시간 복잡도 이내로 끝내야 통과할 수 있습니다. 그 외에도 O(n) × O(logn)처럼 조합되는 알고리즘 또한 이 경우에 해당하므로 생각보다 자주 보게 될 것입니다.

• O(n²): 입력 데이터 수의 제곱만큼 시간을 소모하는 알고리즘입니다. 입력 데이터가 제법 큰(10만 개 이상) 문제에서 이 알고리즘을 사용하면 높은 확률로 시간이 초과됩니다. for 문이 2중 중첩되었거나, 배열끼리 값을 비교/조작하거나, 2차원 배열을 사용한다면 이 정도의 시간이 소요됩니다. 자주 만들고 사용하는 알고리즘이 대부분 여기에 속하므로 ‘이 정도의 시간 복잡도라면 괜찮겠지’라고 생각하면 안 됩니다. 일단 n² 기반으로 연산하면 다른 부가 연산이 필요할 경우 상당히 부담되기 때문에 전략적으로 필요할 때만 수행하는 게 좋습니다.