8.2.3 가우시안 필터

가우시안 분포^{Gaussian distribution}는 자연 현상을 가장 잘 표현하는 이상적인 확률 모형이다. 가우시안 분포는 평균을 중심으로 좌우 대칭의 종 모양 형태로 분포가 줄어드는 형태를 갖는다. 평균이 0이고, 표준 편차가 σ인 1차원 가우시안 분포를 함수 식으로 나타내면 다음과 같다.

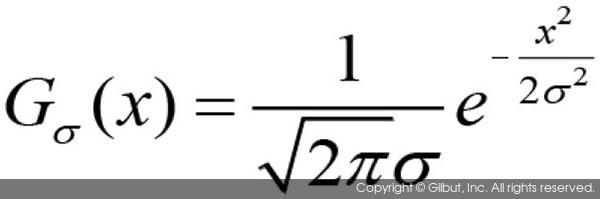
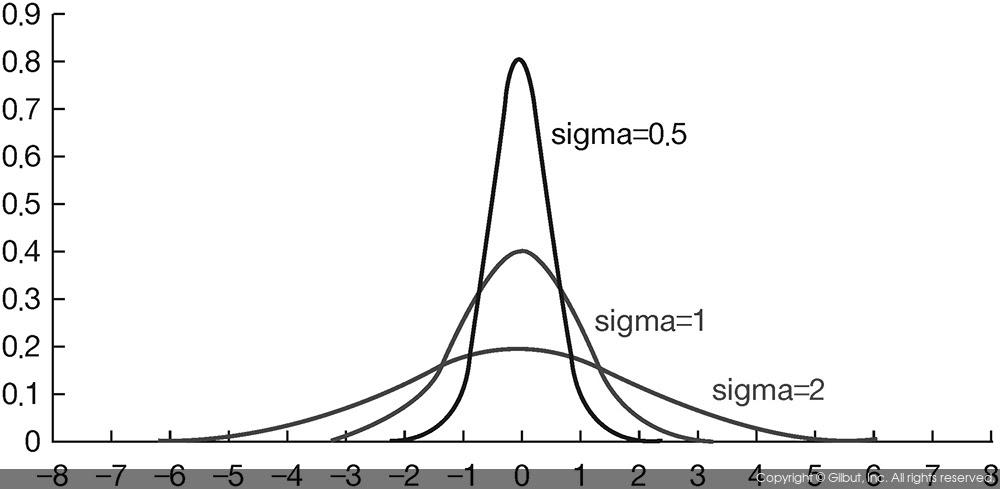
표준 편차 σ가 각각 0.5, 1.0, 2.0인 경우의 가우시안 분포 그래프를 그림 8-9에 나타내었다. 평균이 0인 가우시안 함수이기 때문에 x=0에서 함수 값이 가장 크게 나타나며, 0에서 멀어질수록 함수 값이 감소하게 된다. 그리고 표준 편차 값이 작을수록 뾰족한 곡선을 이루고, 표준 편차가 증가할수록 완만한 곡선을 구성한다. 가우시안 분포에서 함수 값들은 x 값이 -4σ부터 +4σ 사이인 경우에 전체 분포의 99.99%가 존재한다.

영상과 같은 2차원 공간에서 평균이 (0, 0)인 가우시안 함수는 다음과 같이 정의된다.

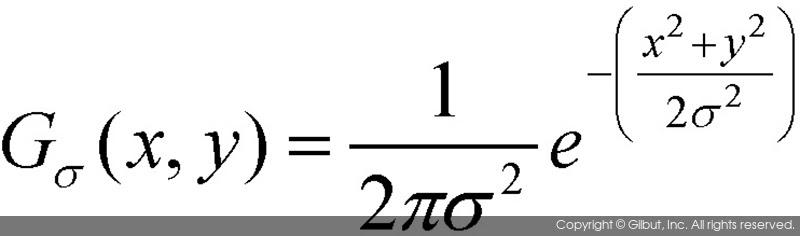
그림 8-10은 σ=1인 경우의 2차원 가우시안 함수 그래프이다. 1차원 가우시안 함수와 마찬가지로 평균인 (0, 0)에서 가장 큰 값을 가지며, 점차 종모양으로 감소하는 곡선의 형태를 이루고 있다.