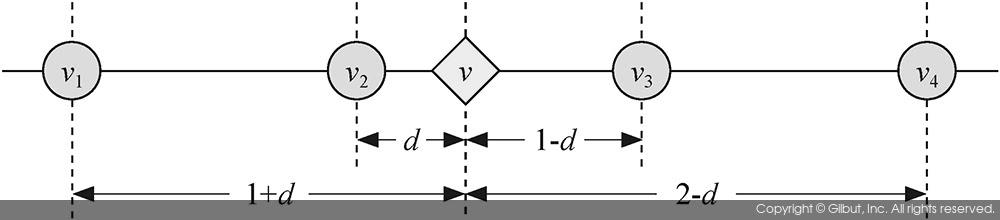
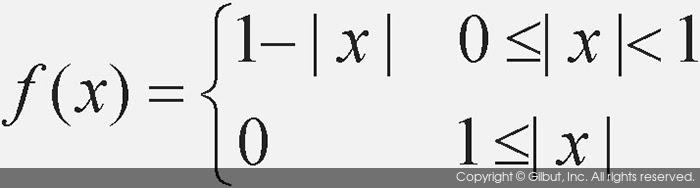좀 더 쉽게 이해할 수 있도록 오직 4개의 점에 대한 3차 회선 보간 방법에 대하여 알아보자. 그림 9-13에서 이미 픽셀 값을 알고 있는 네 개의 좌표는 파란색 원 모양으로 표시하였고, 보간법을 이용하여 픽셀 값을 구하고 싶은 실수 좌표는 노란색 마름모로 표시하였다. 네 개의 정수 좌표의 픽셀 값은 v₁, v₂, v₃, v₄로 표현하였고, 두 번째 픽셀과 실수 좌표 사이의 거리를 d로 나타내었다. d는 0부터 1 사이의 실숫값을 가질 것이다. 이 경우 v₁에 해당하는 픽셀에서의 가중치 값은 f(1+d)로 결정되며, v₂에 해당하는 픽셀에서의 가중치 값은 f(d)로 결정된다. v₃와 v₄에 해당하는 픽셀에 대한 가중치는 각각 f(1-d)와 f(2-d)가 된다. 그러므로 3차 회선 보간법을 이용하여 결정되는 값은 다음의 수식처럼 구할 수 있다.

v = v₁·f(1+d) + v₂·f(d) + v₃·f(1-d) + v₄·f(2-d)

위 수식에 a=-0.5를 대입하면, 3차 회선 가중치 함수는 다음과 같이 정의된다.

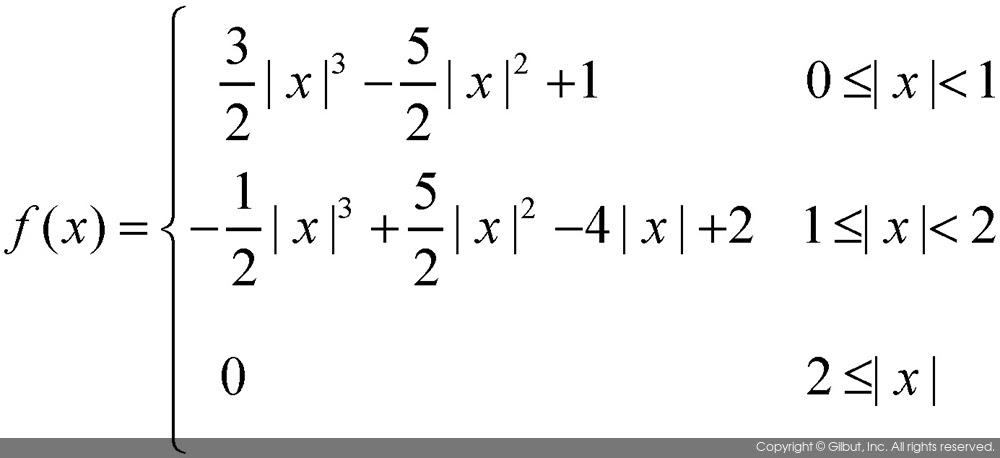
이 함수를 이용하여 보간된 값 v를 계산하면 다음과 같다.

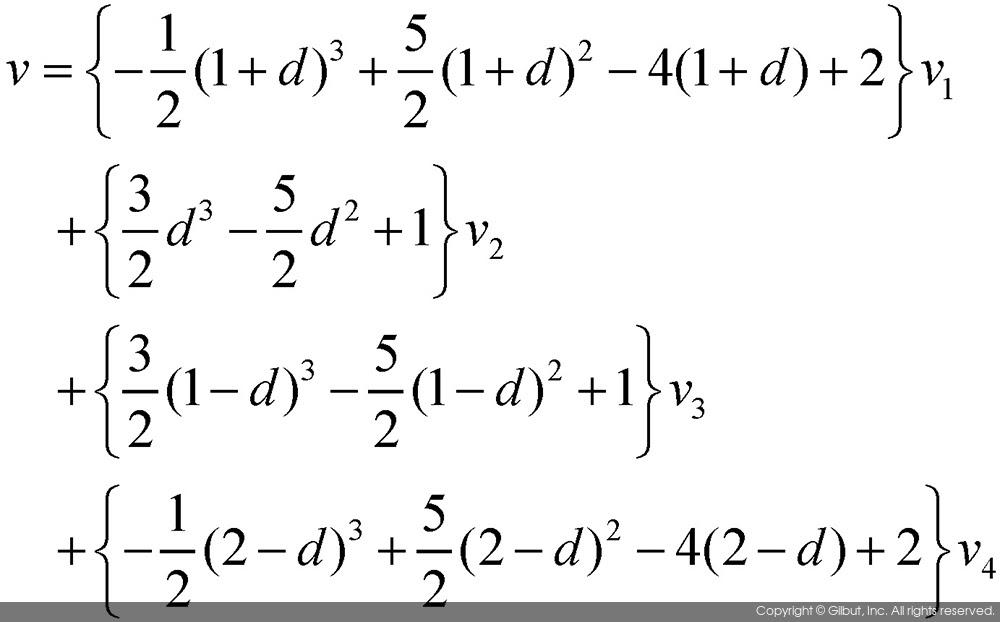
위 식을 모두 전개하여 d에 대한 다항식으로 변환하면 다음과 같이 식이 변형된다.

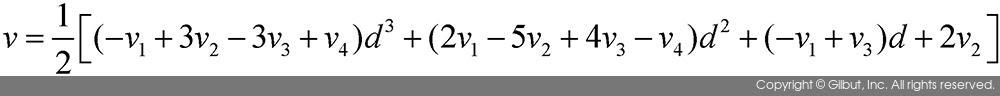
결국 위 수식으로 3차 회선 보간이 이루어지게 되는 것이다. 위 식을 이용하여 4개의 점에 대한 3차 회선 보간을 C/C++ 코드로 작성하면 다음과 같이 나타낼 수 있다.

double p1 = 2 * v2;
double p2 = -v1 + v3;
double p3 = 2 * v1 - 5 * v2 + 4 * v3 - v4;
double p4 = -v1 + 3 * v2 - 3 * v3 + v4;
double v = (p1 + d * (p2 + d * (p3 + d * p4))) / 2.;

Note | 양선형 보간법의 가중치 함수

양선형 보간법으로 픽셀 값을 예측할 때에도 3차 회선 보간법과 마찬가지로 가중치 함수를 이용하는 방법을 사용할 수 있다. 양선형 보간법에서 사용하는 가중치 함수의 형태는 다음과 같다.