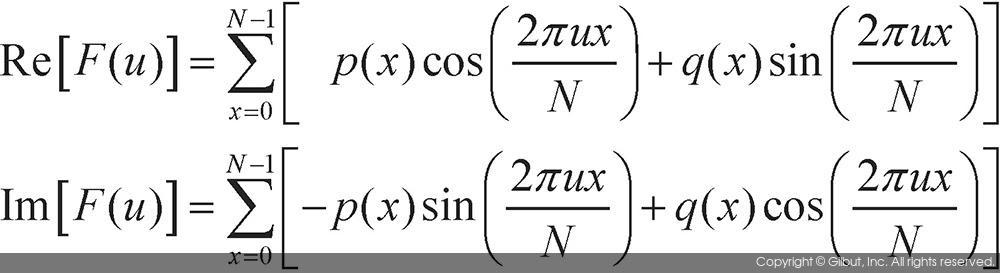푸리에 변환에 의해 생성된 함수 F(u)는 복소수 공간에서 정의된다. 이는 앞의 수식에서 e^jθ는 다음과 같이 수식이 변환되기 때문이다.

e^jθ = cosθ + jsinθ

위 수식을 오일러 공식^{Euler formula}이라고 한다. 그러므로 실제 푸리에 변환을 구현할 때에는 함수 F(u)의 실수부와 허수부를 따로 고려하여 계산해야 한다. 아래 수식은 푸리에 변환 함수의 실수부와 허수부를 따로 나누어 작성한 수식이다.

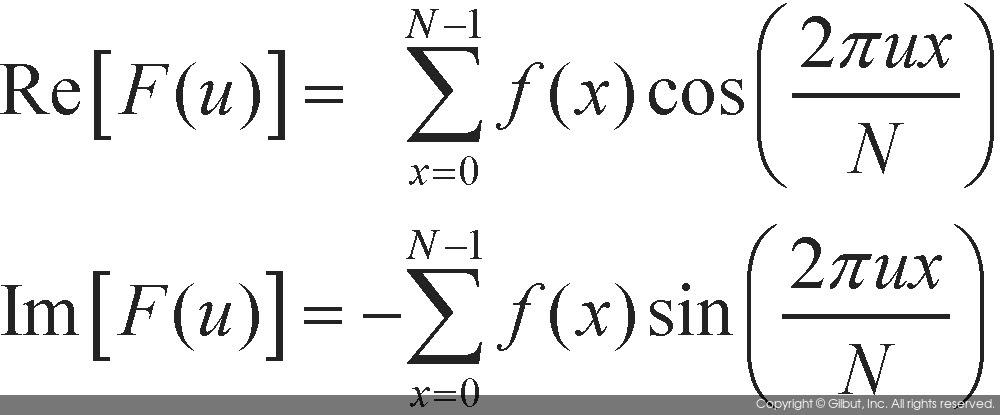
위 수식에서 Re[F(u)]는 함수 F(u)의 실수부를, Im[F(u)]는 함수 F(u)의 허수부를 각각 나타낸다. 삼각함수 공식에서 cos(-θ)=cosθ, sin(-θ)=-sinθ를 만족하기 때문에, 허수부 수식 앞에는 음수 표시가 붙은 것을 볼 수 있다.

만약 입력 함수인 f(x)가 복소수 함수라면 계산식은 더욱 복잡해진다. 예를 들어 f(x)=p(x)+jq(x)라고 가정한다면 이산 푸리에 변환 함수의 실수부와 허수부는 다음과 같이 정의된다.