그림 2-1에서 확인할 수 있듯이 기울기가 4인 함수가 1인 함수보다 가파르게 그려집니다. 이를 이용하면 정의에서 나온 조건인 상수 n₀와 c를 구할 수 있습니다. T(n)=2n+3을 f(n)이라고 하고 g(n)=n이라고 합시다. 그럼 n₀와 c는 굉장히 많은 쌍을 구할 수 있습니다. 그중 한 가지 예로 n₀=3, c=3으로 특정해 보면 그래프는 다음 그림과 같이 그려집니다.

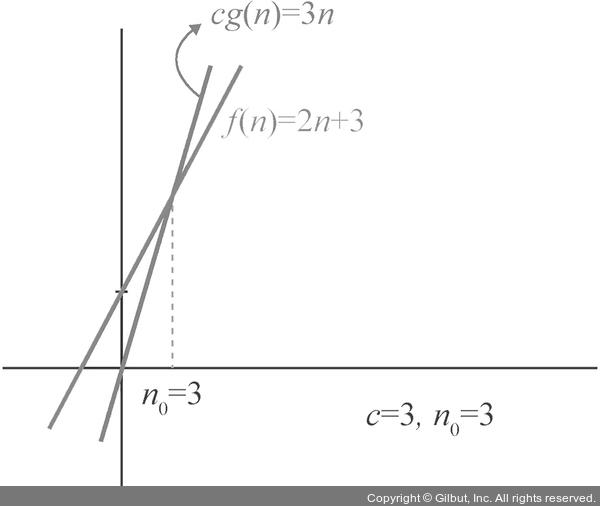
▲ 그림 2-2 정의 이해

cg(n)=3n이 되고 cg(n)과 f(n)이 만나는 지점인 n₀ 이후로는 항상 모든 n에 대해 cg(n) > = f(n)입니다. f(n) > 0도 항상 만족하지요. 이때는 2n+3=O(n)이라고 표기할 수 있는데, g(n)이 n이었고 f(n)이 2n+3이었기 때문입니다. 빅오는 상한(upper bound)을 의미합니다. 2n+3=O(n)은 f(n)=2n+3이 n₀ 이상에서 그래프의 증가 추세가 절대 cg(n)=cn을 넘지 않는다는 것을 보여 줍니다. 그래프를 보면 당연한 이야기이지요.