배열 한 개와 연결 리스트들로 구성되어 있습니다. 정점이 배열의 인덱스가 됩니다. 배열 요소인 연결 리스트는 해당 정점의 인접한 정점의 집합입니다. 정점 0을 보면 인접한 정점들이 {1, 3}이지요. 리스트 요소를 보면 1과 3이 있습니다. 정점 3을 볼까요? 정점 3에 있는 연결 리스트 요소는 {0, 1, 2}입니다. 이는 정점 3에 인접한 정점 집합임을 알 수 있습니다. 이렇게 구현할 때, 두 가지 연산의 빅오를 생각해 봅시다. 먼저 어떤 정점 v에 대해 인접한 모든 노드를 탐색하는 연산을 보죠. 해당 정점을 인덱스로 삼아 배열에서 연결 리스트를 얻어 온 후 이 연결 리스트를 순회하면 됩니다. 이 경우 모든 정점을 조사할 필요 없이 해당 정점의 인접한 정점들만 조사하게 되는군요. 그러므로 빅오는 O(d(v))입니다. 두 번째로 정점 u에 대해 (u, v) ∈ E(G)인지를 검사하는 연산입니다. 이때도 해당 정점을 인덱스로 연결 리스트를 가져와 인접한 모든 노드를 순회해야 하므로 빅오는 O(d(v))입니다.

이번에는 인접 행렬을 알아보겠습니다. 그림을 살펴보세요.

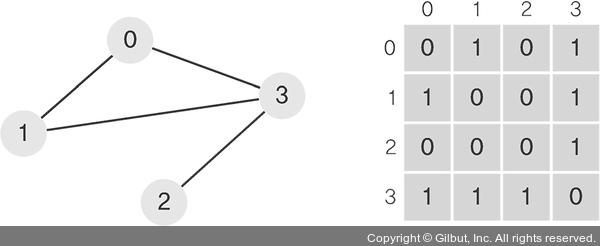
▲ 그림 6-13 인접 행렬