그래프 용어를 정리하면서 신장 부분 그래프(spanning subgraph)를 알아본 적이 있습니다. 이 신장 그래프에서 이 그래프가 트리라면, 다시 말해 사이클이 없는 연결된 그래프라면 이를 신장 트리(spanning tree)라고 합니다. 어떤 그래프가 무방향 그래프(undirected graph)이며 가중치 그래프(weighted graph)라고 합시다. 그래프의 에지에 있는 가중치는 현실 세계에서 비용을 의미합니다. 예를 들어 도로를 건설하는 데 드는 비용이나 어느 도시에서 다른 도시까지 가는 교통비가 될 수도 있습니다. 이 그래프를 신장 트리로 만들려고 합니다. 연결성은 유지하면서 에지의 가중치 합을 최소한으로 만들고 싶습니다.

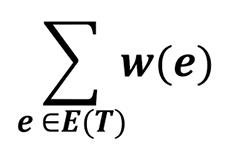
이 식을 최소로 만들고 싶다는 것이죠. 이런 신장 트리를 최소 비용 신장 트리(Minimum cost Spanning Tree), 줄여서 MST라고 합니다. 이 절에서는 MST를 만드는 알고리즘 중 두 가지를 알아보려고 합니다. 크루스칼 알고리즘과 프림 알고리즘입니다.